
大家好,我是机器侠~
在了解逻辑回归之前,我们先简单介绍一下Linear Regression(线性回归)。
线性回归是利用连续性的变量来预估实际数值(比如房价),通过找出自变量与因变量之间的线性关系,确定一条最佳直线,称之为回归线。并且,我们将这个回归关系表示为
Logistic Regression(逻辑回归)
与线性回归不同的是,逻辑回归并不是一个回归算法,它是一个分类算法;通过拟合一个逻辑函数来预测一个离散型因变量的值(预测一个概率值,基于0与1),来描述自变量对因变量的影响程度。自变量可以有一个,也可以有多个。其中,一个自变量被称为一元逻辑回归,而多个自变量被称为多元逻辑回归。
以实例而言,逻辑回归可以预测一封邮件是垃圾邮件的概率是多少。同时,因为结果是概率值,它同样可以对点击率等结果做排名模型预测。
首先,寻找一个合适的预测函数h(x)来预测输入数据的判断结果。其次,构造一个损失函数cost,来表示预测的函数值h(x)与训练集数据类别y的偏差(二者的差值等形式)。对所有训练数据的损失求平均或者求和记为J(θ),表示所有训练数据预测值和世纪类别的偏差。我们很容易得到J(θ)越小,预测得越准确,所以我们的目的就是寻找数J(θ)的最小值。寻找最小值有许多方法,这里我们通过梯度下降法(Gradient Descent)进行展示。
接下来,我们对上述内容进行详细解读:
预测函数:
损失函数 :
损失函数是由逻辑回归的预测函数公式推导而得,值得一提的是,上述的ω^T并不是ω的T次方,而是ω的转置的意思。如果您学习过线性代数的知识应该能很容易理解转置的含义,但没有学习过也没有关系,把它看成ωx使用即可。详细的推导过程不是必须要掌握的知识点,我们会将这部分内容放在文章附录,如果您感兴趣,可以在之后查看。
我们对损失函数进行求导,得到以下结果:
这样一看我们似乎已经完成了逻辑回归的全部内容。但事实上,在机器学习当中,我们的函数常常是多维高阶的,仅仅依靠令导数为 0 然后求解方程的方法往往无法解决问题,所以我们需要另一个方法来寻找损失函数的最小值。通常,我们使用梯度下降的方法
我们可以观察一个最简单的函数
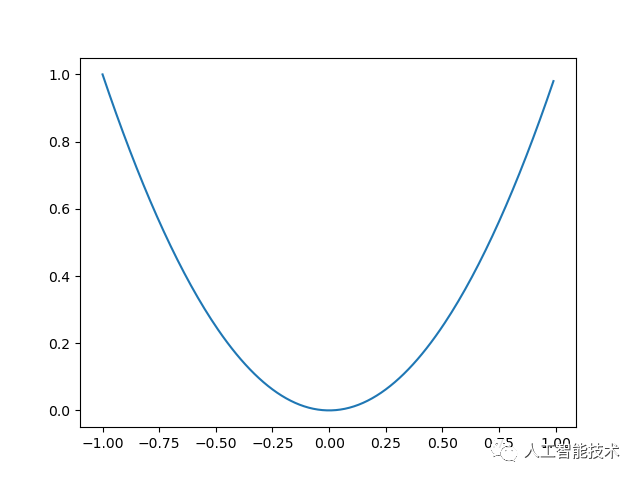
1.首先对 x 取任意一个值比如-0.8,我们可以得到一个 y 值:
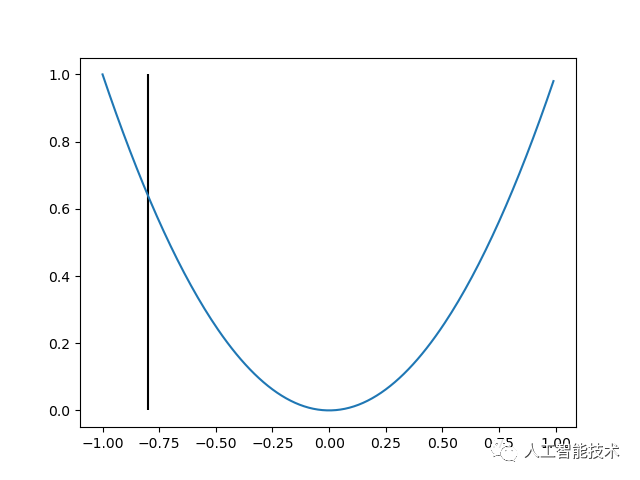
2.其次,求更新方向。例如我们向正方向更新,得到图像如下:
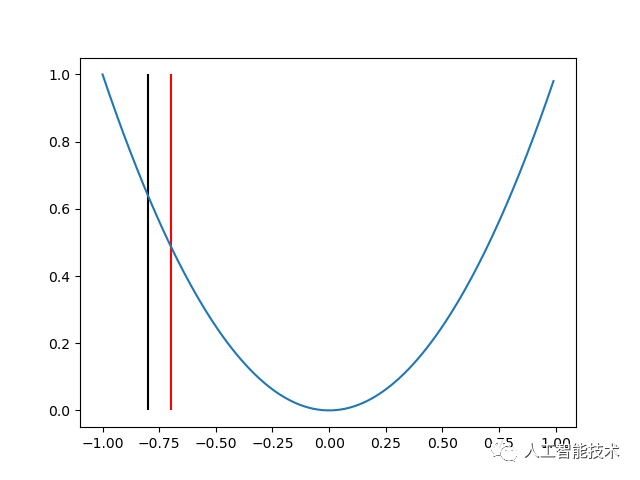
可以发现,当我们向着正方向更新的时候,我们正在逐渐接近最终的结果(零点)。而两次更新之间的间隔(这里是 0.1),在机器学习当中,我们称为学习率。当学习率过大时,x 可能不能很好地收敛;当学习率过小时,x 的收敛速度可能过慢。
3.不断重复第 1、2 步,直到 x 收敛
以上就是梯度下降的主要思想,我们可以得到下降公式:
以鸢尾花分类为例。
# 导入数据
from sklearn.datasets import load_iris
iris = load_iris()
在这里我们先取前两列数据(花萼长度与宽度)进行回归分类
X = iris.data[:,:2]
Y = iris.target
# 将数据划分为训练集和测试集
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(X,Y,test_size=0.2,random_state=0)
# 导入模型,调用逻辑回归 LogisticRegression()函数
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(penalty='l2',solver='newton-cg',multi_class='multinomial')
lr.fit(x_train,y_train)
输出
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, l1_ratio=None, max_iter=100,
multi_class='multinomial', n_jobs=None, penalty='l2',
random_state=None, solver='newton-cg', tol=0.0001, verbose=0,
warm_start=False)
我们详细解释一下 LogisticRegression 中各项参数的定义
penalty:正则化选择参数,默认方式为 L2 正则化
solver:优化算法选择参数,有{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’}四种参数,如果你是用的是 L1 正则化,则只能使用 libinear,这是因为 L1 正则化并不是一个连续可导的损失函数。
muti_class:分类方式选择参数,包括{‘ovr’, ‘multinomial’}两种参数。简单来说,OvR 相对简单,但分类效果相对略差(这里指大多数样本分布情况,某些样本分布下 OvR 可能更好)。而 MvM 分类相对精确,但是分类速度没有 OvR 快。
# 对模型进行评估
print('逻辑回归训练集准确率:%.3f'% lr.score(x_train,y_train))
print('逻辑回归测试集准确率:%.3f'% lr.score(x_test,y_test))
from sklearn import metrics
pred = lr.predict(x_test)
accuracy = metrics.accuracy_score(y_test,pred)
print('逻辑回归模型准确率:%.3f'% accuracy)
输出
逻辑回归训练集准确率:0.850
逻辑回归测试集准确率:0.733
逻辑回归模型准确率:0.733
绘制结果可视化,我们通过两列数据绘制数据集的决策边界。
import numpy as np
lx1, rx1 = X[:,0].min() - 0.5,X[:,0].max() + 0.5
lx2, rx2 = X[:,1].min() - 0.5,X[:,1].max() + 0.5
h = 0.02
x1,x2 = np.meshgrid(np.arange(lx1,rx1,h),np.arange(lx2,rx2,h))
grid_test = np.stack((x1.flat,x2.flat),axis = 1)
grid_pred = lr.predict(grid_test)
grid_pred = grid_pred.reshape(x1.shape)
import matplotlib.pyplot as plt
import matplotlib as mpl
plt.figure(1,figsize=(6,5))
cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
plt.pcolormesh(x1,x2,grid_pred,cmap=cm_light)
plt.scatter(X[:50, 0], X[:50, 1], marker = '*', edgecolors='red', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1], marker = '^', edgecolors='k', label='versicolor')
plt.scatter(X[100:150, 0], X[100:150, 1], marker = 'o', edgecolors='k', label='virginica')
plt.xlabel('Calyx length-Sepal length')
plt.ylabel('Calyx width-Sepal width')
plt.legend(loc = 2)
plt.xlim(lx1.min(), rx1.max())
plt.ylim(lx2.min(), rx2.max())
plt.title("Logical regression of iris classification results", fontsize = 15)
plt.xticks(())
plt.yticks(())
plt.grid()
plt.show()
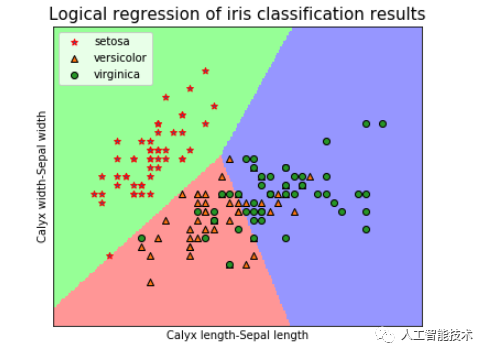
我们可以得到结果:setosa 类线性可分,而 versicolor 类与 virginica 类线性不可分。
我们已经知道,逻辑回归的预测函数 h(x)
假设有 N 个样本,样本的标签有 0 和 1 两类。假设 yi=1 的概率为 pi,yi=0 的概率为 1-pi,基于此,我们可以得到以下公式:
可以发现,当 y 取 0 以及当 y 取 1 的时候,损失函数分别为:
概率求解得到极大似然函数
对该函数取对数可以得到损失函数公式
为什么取对数呢?因为取对数之后,原先的乘法就变成了加法,并且单调性一致,不会改变极值的位置,便于后续的求导。
- EOF -
- 机器学习交流qq群955171419,加入微信群请扫码(读博请说明)