如今Python语言的学习已经上升到了国家战略的层面上。Python语言是人工智能的基础语言,国家相关教育部门对于“人工智能普及”格外重视,不仅将Python列入到小学、中学和高中等传统教育体系中,并借此为未来国家和社会发展奠定了人工智能的人才培养基础,逐步由底层向高层推动“全民学Python”,从而进一步实现人工智能技术的推动和社会人才结构的更迭。

教程背景
近年来,金融领域的量化分析越来越受到理论界与实务界的重视,所谓金融量化,就是将金融分析理论与计算机编程技术相结合,更为有效的利用现代计算技术实现准确的金融资产定价以及交易机会的发现。
在量化金融的时代,选用一种合适的编程语言对于金融模型的实现是至关重要的。在这方面,Python语言体现出了不一般的优势,特别是它拥有大量的金融计算库,极大的缩短了金融量化分析的学习路径。
python在金融中应用的典型事例
讨论一些量化金融中的例子,显示使用Python以及其附属的金融分析库处理起来是多么方便。这些例子是描述性的,对于一些Python语言以及实际应用中的细节问题并不做过多介绍。本讲包括以下几个例子:
隐含波动率:不同到期期限期权的隐含波动率求解并作图,这是很多期权交易者以及风险管理者面对的一项日常任务。
MonteCarlo模拟:通过MonteCarlo模拟来得到一组随时间变化的股票指数,将选择的结果作图,并计算欧式期权的价值。MonteCarlo模拟方法是数值期权定价以及value-at-risk风险管理以及信用价值调整的基础。
技术分析:通过对历史时间序列的分析,完成对一项基于趋势信号的交易策略的回测,专业投资者以及激进的业余投资者通常都会进行这类型的投资分析。
示例演示-隐含波动率
隐含波动率
给定类似于Black-Scholes-Merton(1973)的期权定价公式,隐含波动率是指:在其他条件不变的情况下,通过将这个隐含波动率数值代入到公式中,可以得到不同的执行价格和期限的期权的市场报价。本例中,波动率不是代入到模型或公式中的一个输入参数,而是给定这个公式而得到的一个(数值)优化过程的结果。
这里我们考虑的例子是关于一项新的期权,即基于VSTOXX波动率指数的波动率期权。Eurex是提供基于VSTOXX和各种期货合同的衍生品交易市场,于2013年6月建立了一个综合化的Python为基础的关于这个指数以及基于此指数的衍生品合同的教程,称为”VSTOXXAdvanced Services”。
在讨论VSTOXX期权之前,我们首先回顾一下基于不付息标的欧式看涨期权的Black-Scholes-Merton公式。
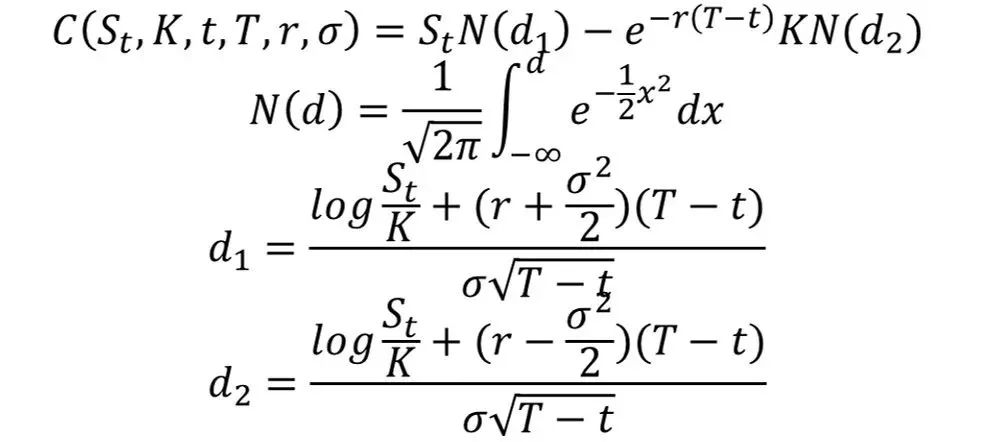
这里,St 代表的资产在t 时刻的价格水平。σ 代表标的资产常数的波动率(即标准差),K 代表期权的执行价格,T 代表期权的到期期限,r 代表常数的无风险短期利率。

现在假设某项欧式看涨期权的报价C*已经给定,那么隐含波动率σ^imp是可以求解上述公式的波动率数值,即:


这个方程并没有显式解,这样需要使用列如Newton等数值方法来估计正确的解。最常用的是Newton方法,使用相关函数的一阶导数,直到达到了规定的迭代次数或者是某种精确性。对于某个初始值 σ^imp 和 0∞:
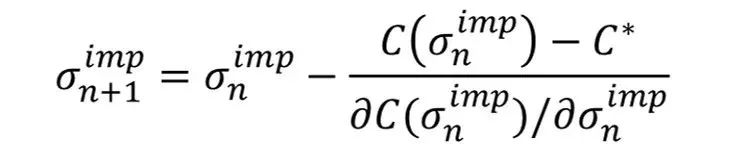
期权定价公式关于波动率的一阶导数称为期权的Vega,由如下公式给出:
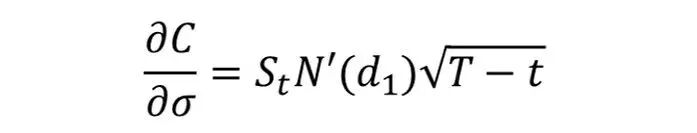
下面我们来分析一种特殊情形 t=0 条件下计算的python代码

当然在这个例子中我们还需要相关的期权报价,以及在我们的关于VSTOXX指数的欧式看涨期权中,我们还需要代码生成single implied volatilities。
T=0,参考日期我们取2014年3月31日,这一天指数的收盘价为 000=17.6639。假设无风险利率 r=0.01 。
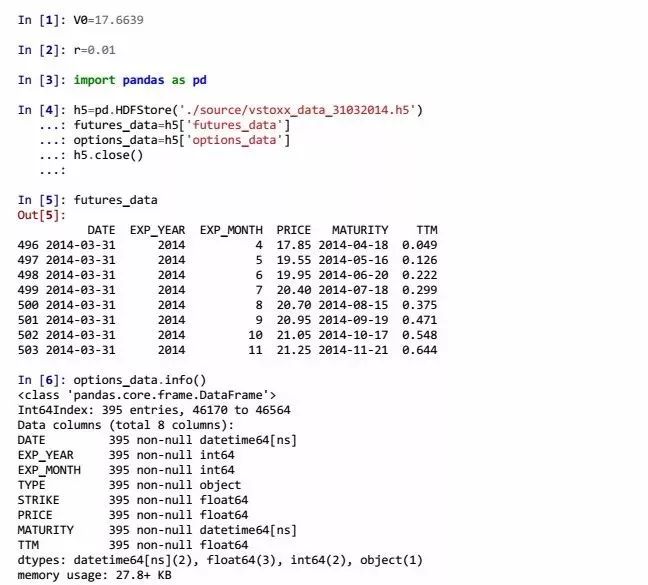
其他参数都来自于期权数据以及需要进行计算获得。数据存储在pandas DataFrame对象中并保存在PyTables数据库文件中。我们需要将它读入内存。
这里之所以需要期货数据,是因为我们需要根据期权的远期moneyness来选择一组VSTOXX期权。在任意时刻交易的VSTOXX期货共有8种,到期日为下面8个月份的第三个星期五。在三月末,期货合同的到期期限是从4月的第三个星期五到11月的第三个星期五。
期权的数据集要更大一些,因为在任意给定的交易日,对于每个到期日,有很多看涨和看跌期权。但是这里到期日与期货是相同的。在2014年3月31日这一天,共有395份看涨期权。
从表中可以看出,交易的看涨期权中有非常实值的(指数的水平比期权执行价格高出很多),也有非常虚值的(即指数的水平比期权执行价格低很多)。因此,我们希望将分析限制在某种给定的(远期)moneyness水平上,给定分别期限的期货价值。假设我们允许期货水平上下50%的波动。
首先,我们定义新的一列来存储结果,并引入我们需要的函数。
现在我们计算看涨期权的隐含波动率。
接着,我们将所选择的期权的隐含波动率用图形表示出来,我们首先取隐含波动率大于0的子集(也就是我们进行了隐含波动率计算的子集)。
为了数据的可视化,我们对于数据集的所有到期日进行迭代,并且将隐含波动率做成线状图或者单点图。因为所有的到期日显示为多个时间,我们需要使用一点技巧来获得没有重复的,排序的日期列表。在Python中,set操作可以去掉重复项目,但是获得的是没有排序的期限集合。因此,我们还要对set进行排序。
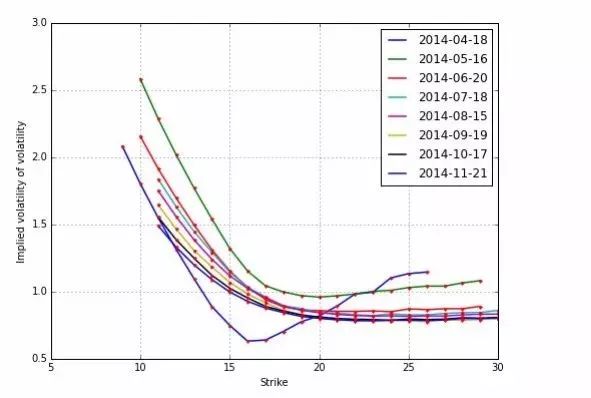
接着我们对所有的日期进行迭代并作图。在这里可以看到一个明显的波动率微笑图形。而且对于长期的期权来说更为明显。
我们来看pandas另外一个强大的功能:对于按照逻辑索引的数据,DataFrame对象options_data都有一个整数的索引。但是这个索引是没有含义的,2014年3月31日交易的期权报价通过期限和执行价格来唯一描述,也就是说每个到期日的每个执行价格水平都对应着唯一的一个看涨期权。
Groupby方法可以得到一个更为有意义的索引,我们可以分别按照MATURITY和STRIKE进行索引。在这个例子中,我们只保留PRICE和IMP_VOL的列。这样的操作会返回一个DataFrameGroupBy对象,为了获得这个数据,我们需要对这个对象进行加总操作。
那么,今天我们就来教大家如何在融行业中使用Python量化分析到此结束,在这过程中能够了解python的功能强大。那么对python量化分析还想了解更多,推荐试听北风网python全栈开发工程师试学课:
基于Python Web框架实现的商城项目
基于Python的微信公众平台开发
基于Django+Bootstrap+Mysql的创客网实战
Python数据分析 - 基于Python实现新闻 爬虫、豆瓣爬虫
Python数据分析 - 基于Python的Scrapy框架和案例需求分析
Python机器学习-手写数字识别
python量化分析
小编在此收集了全世界范围内各大行业最受欢迎的关于人工智能、大数据的学习资料以及课程,。希望小编能帮助到大家找到最适合自己的学习资源。
整理如下:
61本机器人学习电子书、37本大数据电子书、30本人工智能电子书、26本深度学习电子书......各大课程视频、PPT帮助你全面了解行业知识,基础知识掌握必备。
上下滑动查看
由于资料太多,无法在此全部展示,需要这100G学习资料的同学可在【阅读原文】申请哦!
北风网就业情况
每一份努力都值得更好的回报,北风学子经过数月的磨练,现以就业率39%的好成绩回馈他们的努力,其实你也可以!
想要系统的学习python量化分析,北风网帮助你。
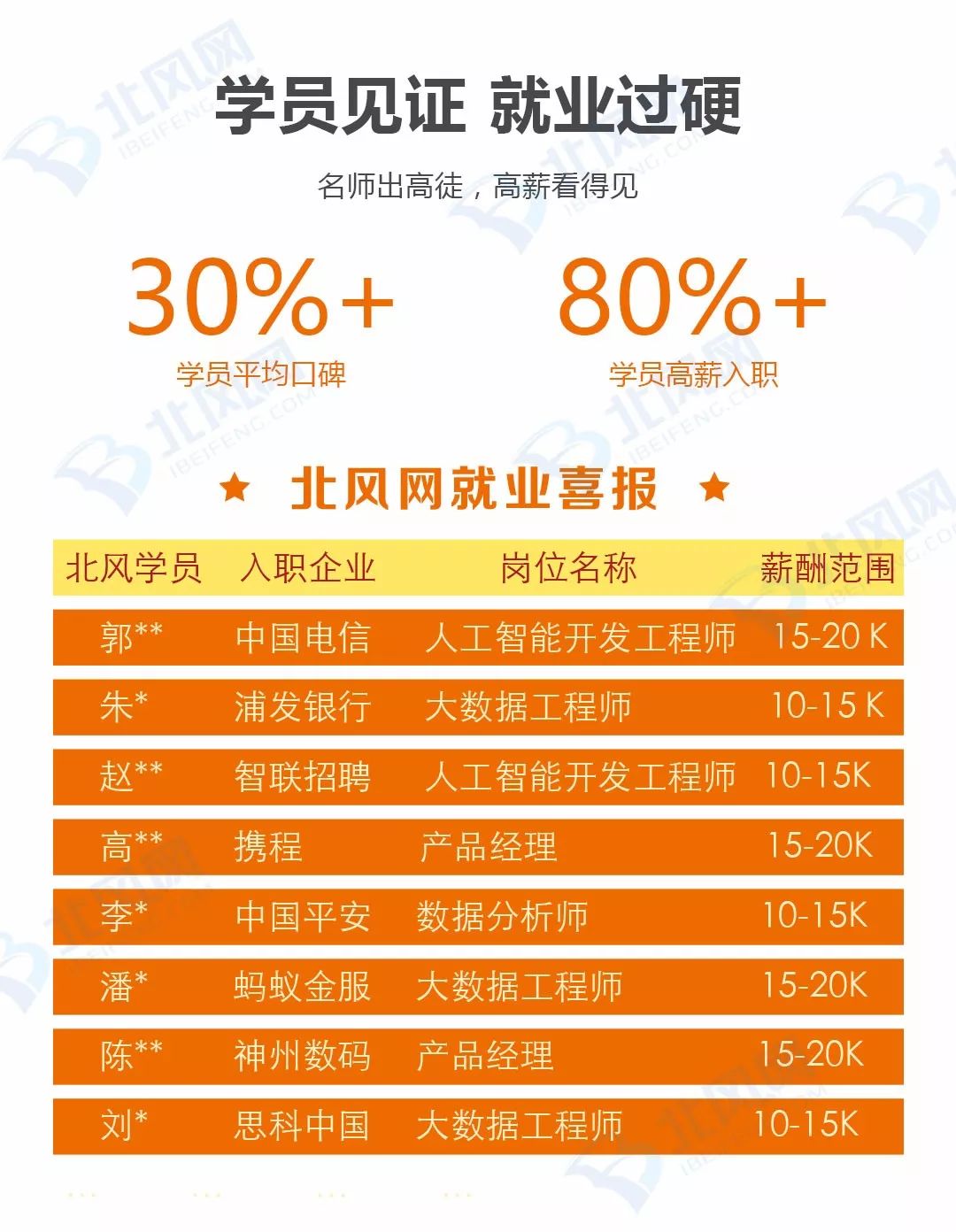
注:由于就业学员签有保密协议,为了给学员造成不必要的麻烦,就业信息有部分隐藏。
结业后,北风网联合阿里云,为合格学员颁发阿里云人才认证证书。
