FCN虽然做出了开创性的工作,FCN-8s相较于此前的SOTA分割表现,已经取得了巨大的优势。但从分割效果上看还很粗糙,对图像的细节处理还很不成熟,也没有考虑到像素与像素之间的上下文(context)关系,所以FCN更像是一项抛砖引玉式的工作,随着U形的编解码结构成为通用的语义分割网络设计范式,各种网络如雨后春笋般涌现。UNet是U形网络结构最经典和最主要的代表网络,因其网络结构是一个U形而得名,这类编解码的结构也因而被称之为U形结构。提出UNet的论文为U-Net: Convolutional Networks for Biomedical Image Segmentation,与FCN提出时间相差了两个月,其结构设计在FCN基础上做了进一步的改进,设计初衷主要是用于医学图像的分割。截至到本书写稿,UNet在谷歌学术上的引用次数已达44772次,堪称深度学习语义分割领域的里程碑式的工作。

在医学图像领域,具体到更加细分的医学图像识别任务时,大量的带有高质量标注的图像数据十分难得,在此之前的通常做法是采用滑动窗口卷积(类似于图像分块)的方式来进行图像局部预测,这么做的好处是可以做图像像素做到一定程度定位,其次就是滑窗分块能够使得训练样本量增多。但缺点也很明显,一个是滑窗操作非常耗时,推理的时候效率低下,其次就是不能兼顾定位精度和像素上下文信息的利用率。UNet在FCN的基础上,完整地给出了U形的编解码结构,如下图所示。
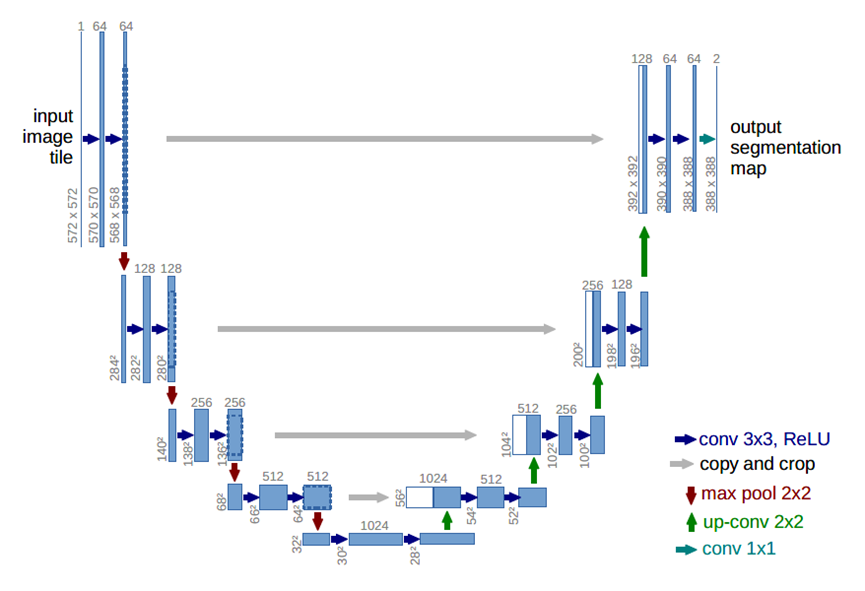
UNet结构包括编码器下采样、解码器上采样和同层跳跃连接三个组成部分。编码器由4组卷积、ReLU激活和最大池化构成,每一组均有两次3*3的卷积,每个卷积层后面都有一次ReLU激活函数,然后再进行一次步长为2的2*2最大池化进行下采样,如第一组操作输入图像大小为572*572,两轮3*3的卷积之后的特征图大小为568*568,再经过22最大池化后的输出尺寸为284*284。解码器由4组2*2转置卷积、3*3卷积构成和一个ReLU激活函数构成,在最后的输出层又补充了一个1*1卷积。最后是同层跳跃连接,这也是UNet的特色操作之一,指的是将下采样时每一层的输出裁剪后连接到同层的上采样层做融合。每一次下采样都会有一个跳跃连接与对应的上采样进行融合,这种不同尺度的特征融合对上采样恢复像素大有帮助,具体来说就是高层(浅层)下采样倍数小,特征图具备更加细致的图特征,低层(深层)下采样倍数大,信息经过大量浓缩,空间损失大,但有助于目标区域(分类)判断,当高层和低层的特征进行融合时,分割效果往往会非常好。从某种程度上讲,这种跳跃连接也可以视为一种深度监督。
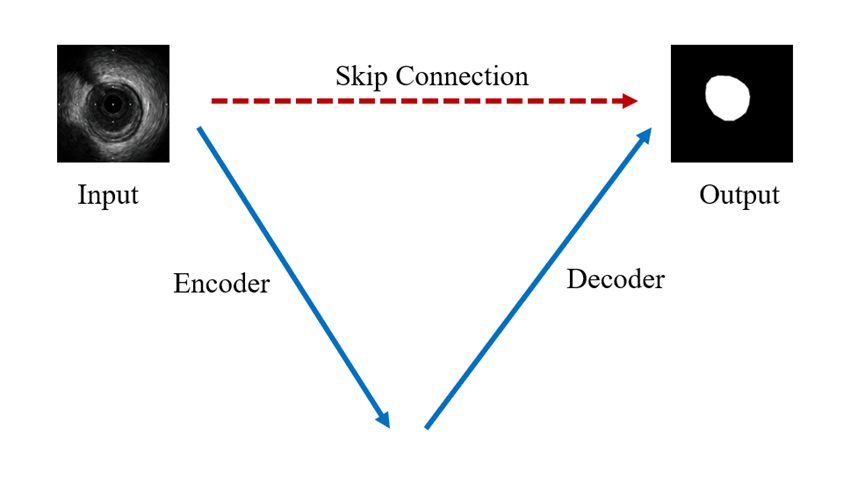
我们将UNet结构按照编码器、解码器和同层跳跃连接进行简化,如下图所示。编码器下采样用于特征提取和语义信息浓缩,解码器上采样用于图像像素恢复,跳跃连接则用于信息补充。自此,基于U形结构的编解码设计成为深度学习语义分割中的奠基性的网络结构,经过近几年的发展,语义分割虽然取得了长足的进步,但UNet和编解码结构一直是新的模型设计的参照对象。
下述代码给出了UNet结构的一个简易实现版本。我们先分别搭建了包含卷积和ReLU的编码块和解码块,然后在编解码块的基础上搭建完整的UNet结构,在前向计算流程中补充同层跳跃连接。
import torchimport torch.nn as nnimport torch.nn.functional as F
class UNetEnc(nn.Module): def __init__(self, in_channels, out_channels, dropout=False): super().__init__() layers = [ nn.Conv2d(in_channels, out_channels, 3, dilation=2), nn.ReLU(inplace=True), nn.Conv2d(out_channels, out_channels, 3, dilation=2), nn.ReLU(inplace=True), ] if dropout: layers += [nn.Dropout(.5)] layers += [nn.MaxPool2d(2, stride=2, ceil_mode=True)] self.down = nn.Sequential(*layers) def forward(self, x): return self.down(x)
class UNetDec(nn.Module): def __init__(self, in_channels, features, out_channels): super().__init__() self.up = nn.Sequential( nn.Conv2d(in_channels, features, 3), nn.ReLU(inplace=True), nn.Conv2d(features, features, 3), nn.ReLU(inplace=True), nn.ConvTranspose2d(features, out_channels, 2, stride=2), nn.ReLU(inplace=True), ) def forward(self, x): return self.up(x)
class UNet(nn.Module): def __init__(self, num_classes): super().__init__()
self.enc1 = UNetEnc(3, 64) self.enc2 = UNetEnc(64, 128) self.enc3 = UNetEnc(128, 256) self.enc4 = UNetEnc(256, 512, dropout=True) self.center = nn.Sequential( nn.Conv2d(512, 1024, 3), nn.ReLU(inplace=True), nn.Conv2d(1024, 1024, 3), nn.ReLU(inplace=True), nn.Dropout(), nn.ConvTranspose2d(1024, 512, 2, stride=2), nn.ReLU(inplace=True), ) self.dec4 = UNetDec(1024, 512, 256) self.dec3 = UNetDec(512, 256, 128) self.dec2 = UNetDec(256, 128, 64) self.dec1 = nn.Sequential( nn.Conv2d(128, 64, 3), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 3), nn.ReLU(inplace=True), ) self.final = nn.Conv2d(64, num_classes, 1)
def forward(self, x): enc1 = self.enc1(x) enc2 = self.enc2(enc1) enc3 = self.enc3(enc2) enc4 = self.enc4(enc3) center = self.center(enc4) dec4 = self.dec4(torch.cat([ center, F.upsample_bilinear(enc4, center.size()[2:])], 1)) dec3 = self.dec3(torch.cat([ dec4, F.upsample_bilinear(enc3, dec4.size()[2:])], 1)) dec2 = self.dec2(torch.cat([ dec3, F.upsample_bilinear(enc2, dec3.size()[2:])], 1)) dec1 = self.dec1(torch.cat([ dec2, F.upsample_bilinear(enc1, dec2.size()[2:])], 1)) return F.upsample_bilinear(self.final(dec1), x.size()[2:])
-
机器学习交流qq群955171419,加入微信群请扫码