深度学习基础系列 | 损失函数

本系列的目的是帮助大家可以在不使用任何深度学习框架的情况下，实现神经网络的反向传播算法。因此从本篇开始，我们将逐步实现手写算法的各个功能。首先学习最常使用的两个损失函数，SigmoidCrossEntropyLoss和SoftmaxCrossEntropyLoss，损失函数虽然是模型推理后才会使用到，但其作用是计算网络模型每次迭代的前向计算结果与真实值的差距，从而指导下一步的训练向正确的方向进行。因此小编放到最开始讲，这样才能更加清楚我们的模型到底在做什么以及期望得结果。

花一点时间，学一点东西

1. 介绍

SigmoidCrossEntropyLoss我们在上一篇逻辑回归中已经使用过。这里再看一下sigmoid的函数图像，模型输出的结果经过sigmoid函数后可以被压缩到(0-1)之间，但sigmoid在变量取非常大的正值或负值时会出现饱和现象。

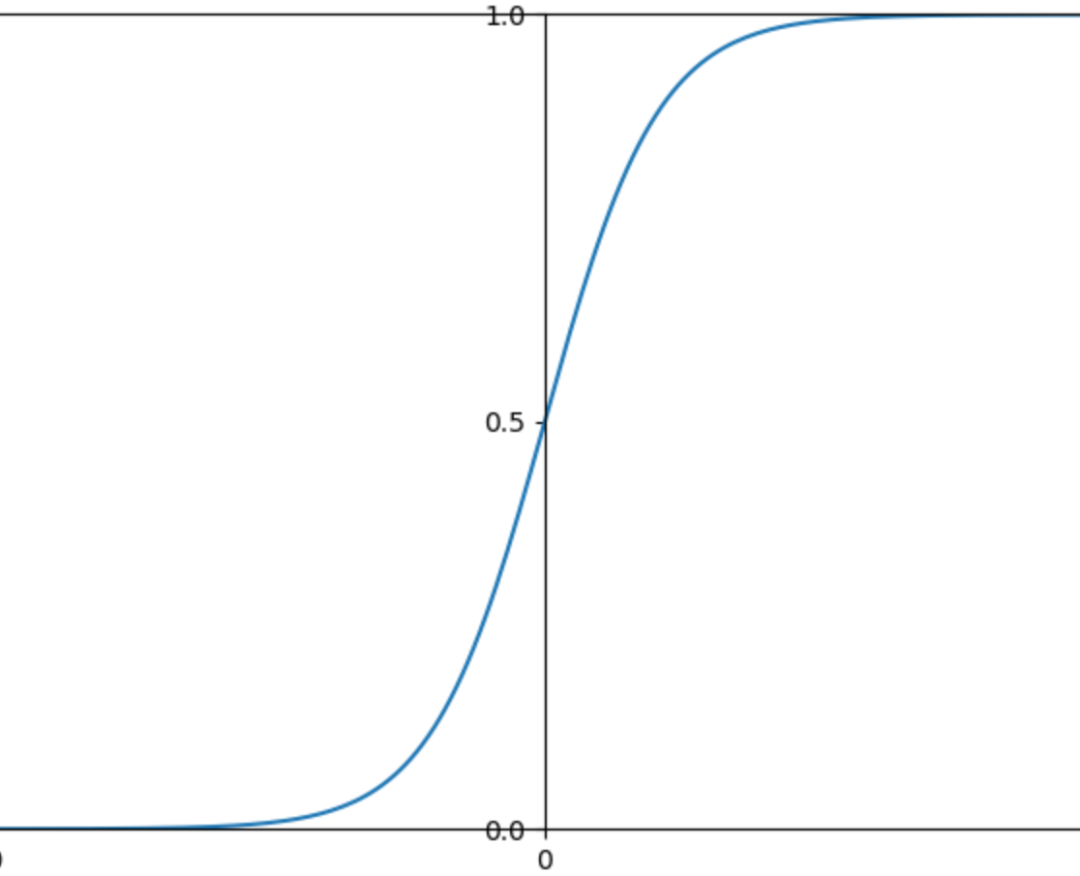
关于sigmoid损失函数公式我们已经推导过了：

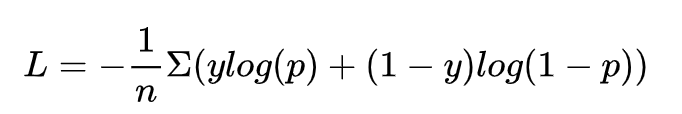
常用于二元分类的问题，输出结果表示分类为目标的概率P和不是该目标的概率(1-P)。

SoftmaxCrossEntropyLoss，也叫归一化指数函数，是经常在多分类问题中使用的损失函数，也是深度学习变种最多的函数之一。我们在度量学习中使用的arcfaceloss、AMSoftmax等函数都是基于此优化的。损失函数公式如下(仍然可由对数似然推导出来，这里就不再赘述)：

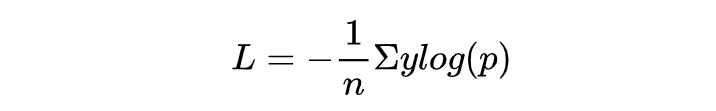
Softmax损失函数在多分类问题中不但可以将输出结果转为非负值，并且使得预测结果的概率之和为1。

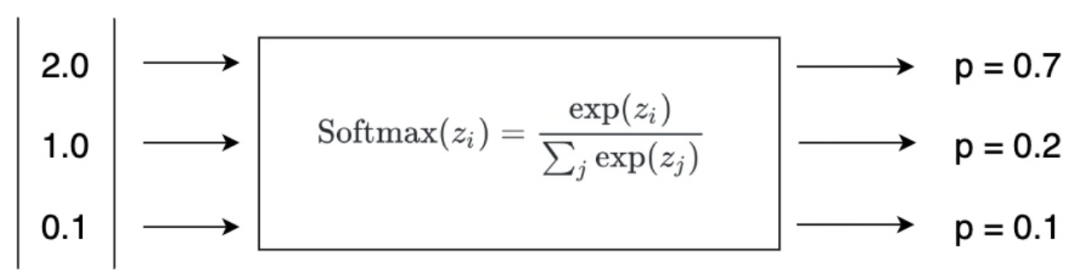
2. 溢出问题

2.1 关于sigmoid精度溢出问题

x的取值可能>=0，也可能<0。 在计算机中，np.exp(1000)会上溢，而np.exp(-1000)为0.0，不会溢出。

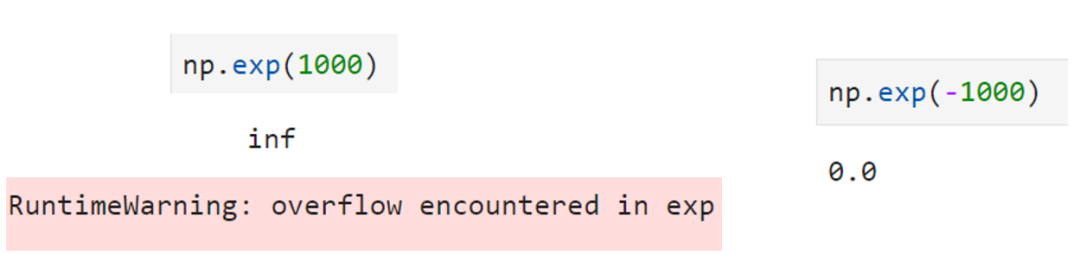
利用这一特性，可以对sigmoid进行改写。

分子分母同乘以。此时，当x<0时不会溢出。

2.2 关于softmax的溢出问题

同样的，我们只考虑x大于0的场景，怎样可以使得不会溢出呢？我们可以给函数分子分母同乘以，而这个n便是max(x)求得。

此时便转换为

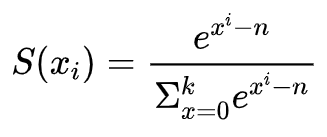
3. SoftmaxCrossEntropy求导

网上大部分都是纯粹的数学公式去推到softmax的导数，我们这里将演示在实际使用中，将类别标签改为one-hot形式后SoftmaxCrossEntropy是如何求导的。

3.1 思路：

• 确定预测的值Y是1x3维度，确定标签T是1x3维度。根据此描述对loss进行标量式推导，然后推广到更多情况；
• softmax函数，由于分母是sum（所有元素），所以对每个元素求导时，都要加上其他元素上的导数。

3.2 求解

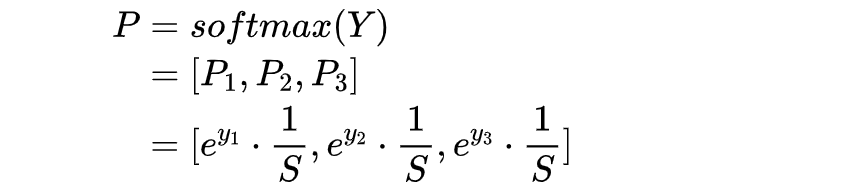
• 标签的定义为：，比如是onehot，label=1，则

• Loss的定义为：

• 计算y1导数

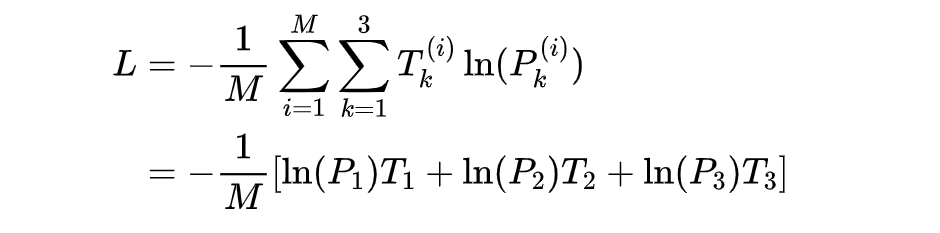
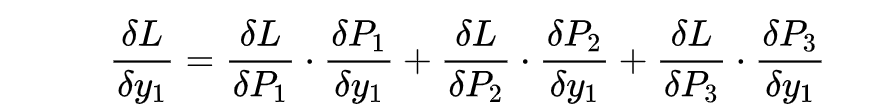
4. 代码实现

• SigmoidCrossEntropyLoss

class SigmoidCrossEntropy(Module):
    def __init__(self, params, weight_decay=1e-5):
        super().__init__()
        self.params = params
        self.weight_decay = weight_decay
        
    def sigmoid(self, x):
        p0 = x 0
        p1 = ~p0
        x = x.copy()
        x[p0] = np.exp(x[p0]) / (1 + np.exp(x[p0]))
        x[p1] = 1 / (1 + np.exp(-x[p1]))
        return x
 
    def forward(self, x, label_onehot):
        eps = 1e-6
        self.label_onehot = label_onehot
        self.predict = self.sigmoid(x)
        self.predict = np.clip(self.predict, a_max=1-eps, a_min=eps)  # 裁切
        self.batch_size = self.predict.shape[0]
        return -np.sum(label_onehot * np.log(self.predict) + (1 - label_onehot) * 
                        np.log(1 - self.predict)) / self.batch_size
    
    def backward(self):
        self.decay_backward()
        return (self.predict - self.label_onehot) / self.batch_size

• SoftmaxCrossEntropyLoss

class SoftmaxCrossEntropy(Module):
    def __init__(self):
        super().__init__()
        
    def softmax(self, x):
        max_x = np.max(x, axis=1, keepdims=True)
        exp_x = np.exp(x - max_x)
        return exp_x / np.sum(exp_x, axis=1, keepdims=True)




    
    def forward(self, x, label_onehot):
        eps = 1e-6
        self.label_onehot = label_onehot
        self.predict = self.softmax(x)
        self.predict = np.clip(self.predict, a_max=1-eps, a_min=eps)  # 裁切
        self.batch_size = self.predict.shape[0]
        return -np.sum(label_onehot * np.log(self.predict)) / self.batch_size
    
    def backward(self):
        return (self.predict - self.label_onehot) / self.batch_siz