
基本信息
作者:Wan-Duo Kurt Ma, J.P. Lewis, W. Bastiaan Kleijn
机构:Victoria University
摘要
本文提出了一种不需要反向传播就可以训练深度神经网络的方法,称为HSIC(希尔伯特-施密特独立性准则)信息瓶颈。HSIC信息瓶颈可以缓解反向传播中出现的梯度消失和梯度爆炸问题,从而可以训练非常深的网络而不需要跳过连接。此外,HSIC信息瓶颈也不需要对称的反馈或层间的参数锁定。在MNIST/FashionMNIST/CIFAR10数据集上的实验表明,即使不要求网络输出与标签相似,HSIC信息瓶颈也可以达到与反向传播训练模型相当的分类性能。在HSIC信息瓶颈训练的基础上添加一个单层网络继续用SGD训练(不用反向传播),性能可以进一步提升。
介绍
尽管SGD和反向传播算法目前主导了深度学习,但研究者也探索了其它优化算法,例如:
- Kickback:沿着全局单类错误的方向追踪局部梯度
- Feedback alignment:显示可以用随机反馈连接训练深度神经网络
- Alternating minimization:将嵌套目标分解为子问题,允许层并行更新
但它也存在一些问题,如计算时间长、梯度消失和爆炸、需要层间顺序计算和参数锁定等。与此同时,反向传播也被认为与生物学认知不符。因此研究深度学习的理论和实际替代方案尤为重要。
信息论为学习理论和神经科学研究提供了基础。信息瓶颈(IB)原则将最小充分统计量的概念推广到了表示层之间的信息量损失和保留的权衡上。「但是IB原则在深度神经网络中的计算存在实际困难」,例如输入的连续性导致互信息为无穷,离散化带来的维数灾难等。已有的应用IB原则训练深度神经网络的方法需要对互信息进行近似。
「本文将IB中的互信息量替换为HSIC,后者可以稳健地度量统计(独)立性,时间复杂度仅为」,部分规避了维数灾难。我们提出了HSIC信息瓶颈训练方法,在多个标准分类问题上获得了与反向传播训练性能相当的结果。这为无反向传播深度学习提供了一个可行途径
本文方法
图1展示了HSIC信息瓶颈网络的架构。图1a)是标准的前馈全连接网络,通过HSIC信息瓶颈目标函数进行训练,可以获得最后一层包含分类信息的隐层表示。图1b)展示了多尺度网络架构。其中每个分支HSIC-net_σi都是用特定的σ参数训练的HSIC信息瓶颈网络。汇聚层(Aggregator)对所有分支的输出特征进行平均,形成最终的输出表示,输入到后续的格式化训练中。
多尺度结构的设计原因是:
HSIC计算依赖于核函数的σ参数,不同尺度的σ适合检测不同范围的依赖性多个尺度的HSIC网络融合,可以提供更全面的信息,提升格式化训练的效果所以图1展示了两种架构:单模型的HSIC信息瓶颈网络,以及融合多尺度模型的汇聚结构。它们都避免了反向传播,可以用于无监督表示学习。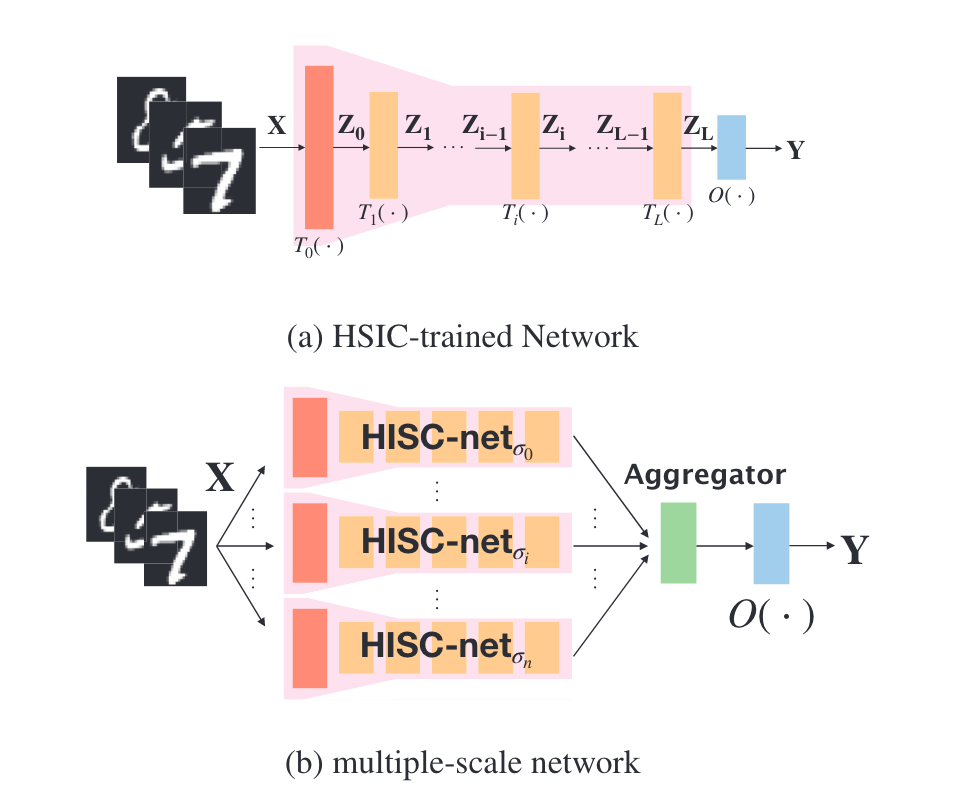
HSIC信息瓶颈
假设我们有一个由L个隐层组成的网络:
将互信息量替换为HSIC,我们可以得到HSIC信息瓶颈目标函数:
其中分别是输入和标签,控制两项的权重。
根据HSIC的公式,每一项可以写成:
其中是中心化的HSIC核矩阵。
这个目标函数鼓励学习的隐层表示
在移除与输入无关的信息以避免过拟合的同时,保留预测标签需要的信息。
我们对每个层独立优化这个目标函数,进行层级的坐标下降,不进行梯度反向传播。
无格式训练
将最后一层的大小设置为类别数,只用HSIC信息瓶颈目标函数训练,可以直接产生one-hot的输出,通过固定的排列即可用于分类,无需额外的格式化过程。

格式化训练
在无格式训练的网络后面添加一个输出层,带softmax函数,用于分类。固定无格式训练的网络,只训练新添加的输出层,用交叉熵损失函数。
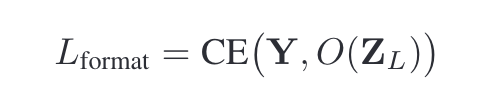
多尺度网络
用不同的HSIC内核参数训练多个网络,将它们的输出表示进行平均,输入到格式化训练中,可以获得更好的结果。
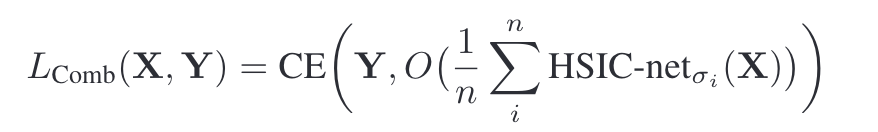
实验结果
在MNIST/FashionMNIST/CIFAR10数据集上,无格式训练的结果与反向传播训练的模型相当。
深层网络上,反向传播效果很差,而HSIC信息瓶颈不会遇到梯度消失问题,仍然有不错的效果。
结论
本文证明了可以不用反向传播,通过HSIC信息瓶颈训练深度分类网络,获得竞争的结果。
HSIC信息瓶颈可以缓解反向传播中的梯度问题,不需要对称反馈和层间锁定。
HSIC信息瓶颈为无反向传播的深度学习提供了一个有效途径。
尽管本文的方法不是为了达到当前的最佳性能,但它打开了一种全新的深度学习范式的可能性。未来的工作可以考虑改进HSIC内核的参数,在不同的任务上评估这种方法。总之,这项研究指明了一个可行的方向,即不依赖反向传播也可以进行有效的深度学习。