反应堆压力容器(RPV)钢在使用过程中暴露于高能中子会发生脆化。屈服应力(Δσy)的增加会导致脆性到韧性转变温度(ΔTc)的相应增加。大多数现有模型对试验反应堆中加速辐照后较高频率下的ΔTc预测不足。高辐照度(在某些情况下高达 1020n/cm2)将在 RPV 容器延长运行80 年或更长时间后,在低品位辐照度条件下达到。脆化问题已在加速的高通量试验反应辐照中得到广泛研究。然而,试验反应堆数据的使用自然会产生辐照影响的问题。
来自我国台湾成功大学的学者使用机器学习方法对一组硬化数据进行训练,涵盖了广泛的辐照度、辐照度和钢成分,以确定辐照和材料变量对 Δσy 的交互影响。分析包括基于机器学习的六种核心钢(即 CM6、LC、LD、LG、LH 和 LI)的Δσy变量依赖性交叉图,其铜和镍含量存在受控差异。主要目的是评估有效与实际浮力(ɸte/ɸt)的比率,作为浮力、浮力和钢成分的函数。这些信息对于在校准低通量-高通量脆化模型时正确使用中间通量-高通量数据至关重要。预测的ɸte/ɸt 与之前基于物理学的溶质重组捕集模型得出的估计值相当一致。相关文章以“Characterizing the flux effect on the irradiation embrittlement of
reactor pressure vessel steels using machine learning”标题发表在Acta Materialia。
论文链接:
https://doi.org/10.1016/j.actamat.2023.119144

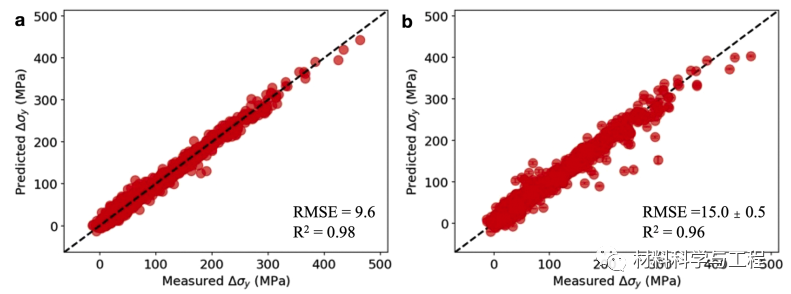
图 1. (a)全尺度(RMSE = 9.6;RMSE/σ = 0.13;R2 =0.98)、(b)5 倍 CV(RMSE = 15.0 ± 0.5;RMSE/σ = 0.20 ± 0.00;R2 =0.96)的奇偶图。每个图中显示的实验数据数量为 1490 个。
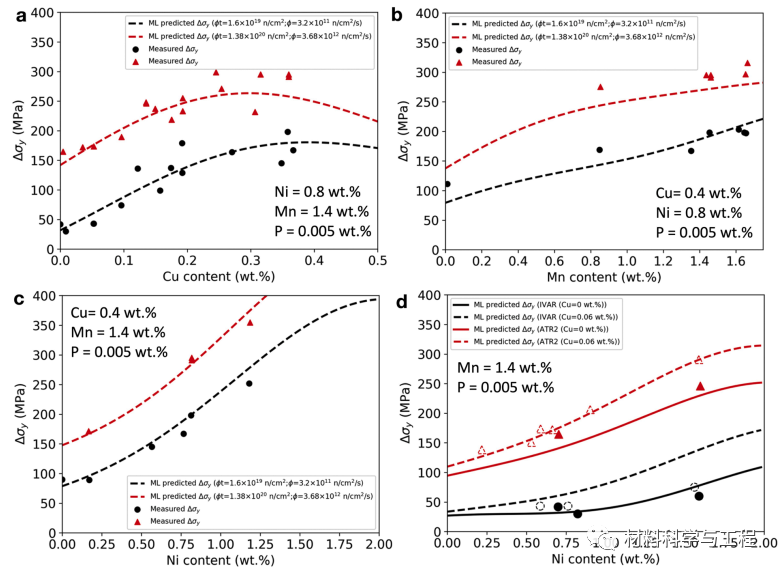
图 2.(a-d) 290℃ 时 (a) 铜、(b) 锰和 (c, d) 镍的成分 Δσy 交叉图: (a)铜、(b)锰和(c, d)镍在 IVAR 的影响//通量为 1.6 ×
1019 n/cm2//3.2 × 1011 n/cm2/s 和 ATR-2 的影响//通量为 1.38
× 1020 n/cm2//3.68 × 1012 n/cm2/s。各图中显示的实验数据数量分别为 (a) 30、(b) 13、(c)
10 和 (d)14。
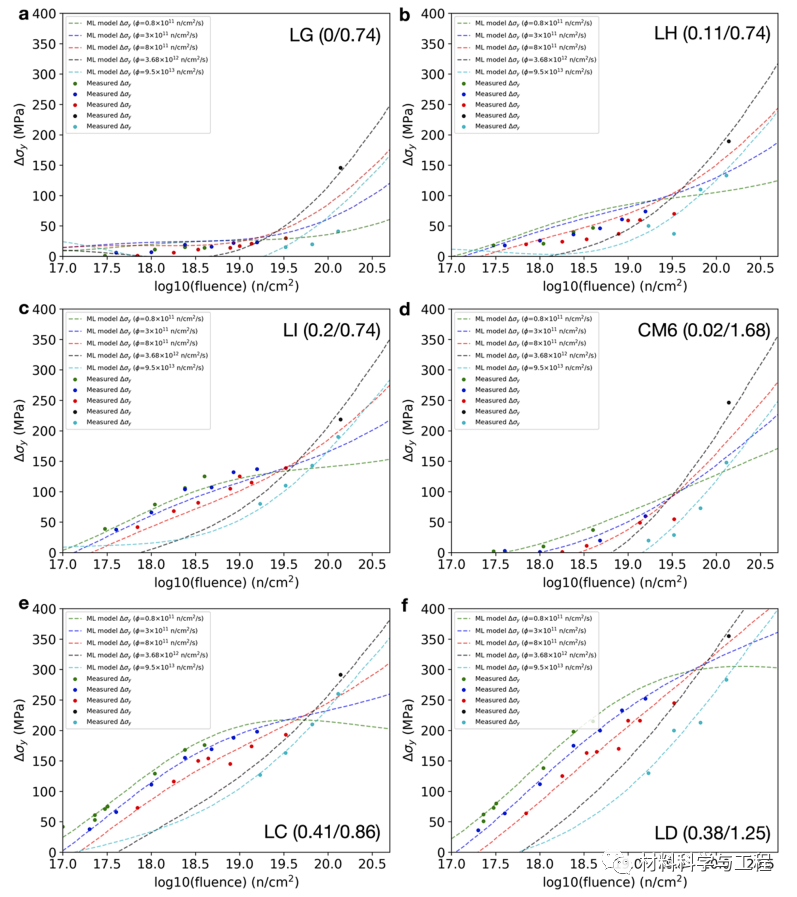
图 3. 核心合金在 290℃ 温度下不同熔点下的对数熔点-Δσ
y 交叉图。各图中显示的实验数据数量分别为 (a) 22、(b) 22、(c) 22、(d) 17、(e) 28 和 (f) 28。
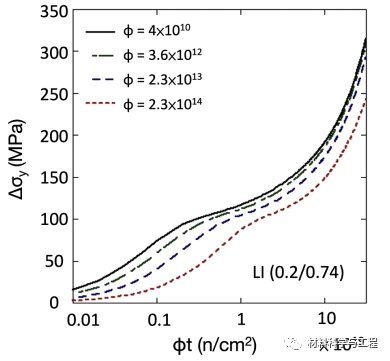
图 4. 以物理为基础的阿夫拉米模型预测的 LI (0.2/0.74) 硬度随通量变化的图示
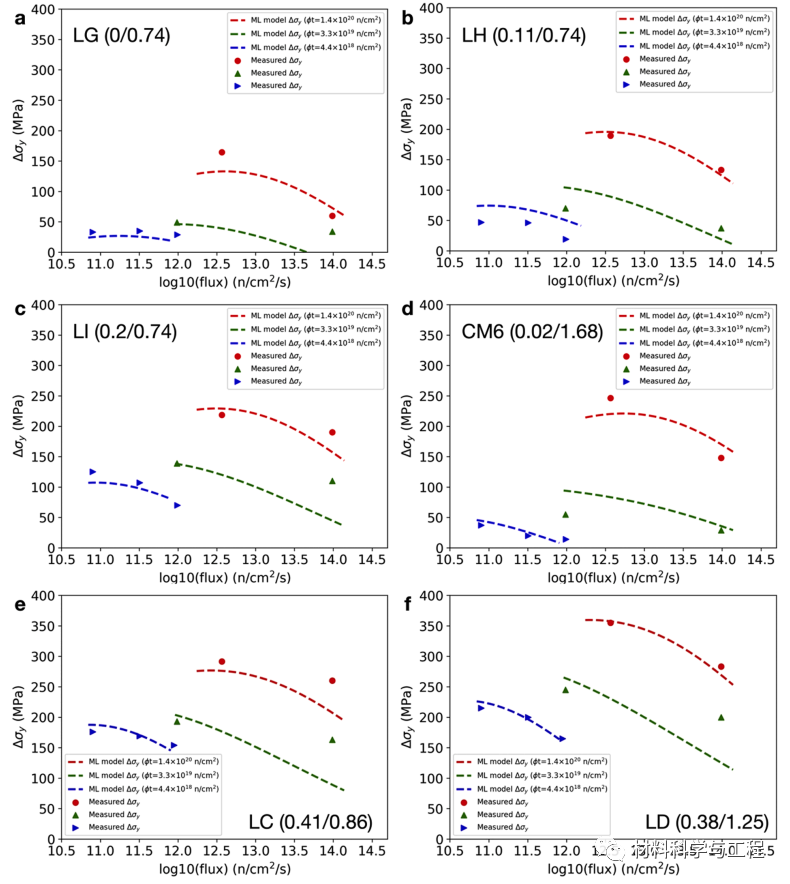
图 5. 在 290℃ 温度条件下,核心合金和不同熔剂的对数通量-Δσy交叉图。每个图中显示的实验数据数量为 7。
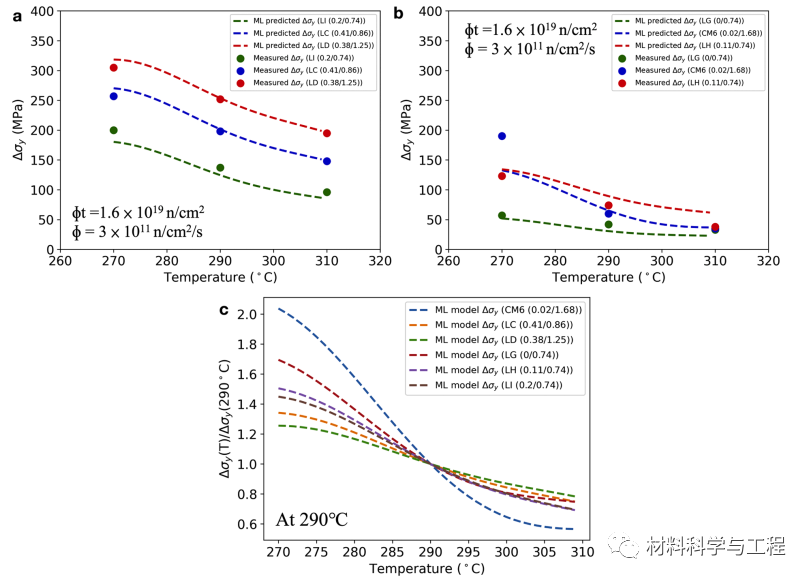
图 6:(a 和 b)核心合金在 1.6 × 1019n/cm2、3 × 1011 n/cm2/s下的Δσy 辐照温度横坐标图;以及(c)Δσy(T)/Δσy(290℃) 与温度的关系图。在(a) 和 (b) 中显示的实验数据数为9。
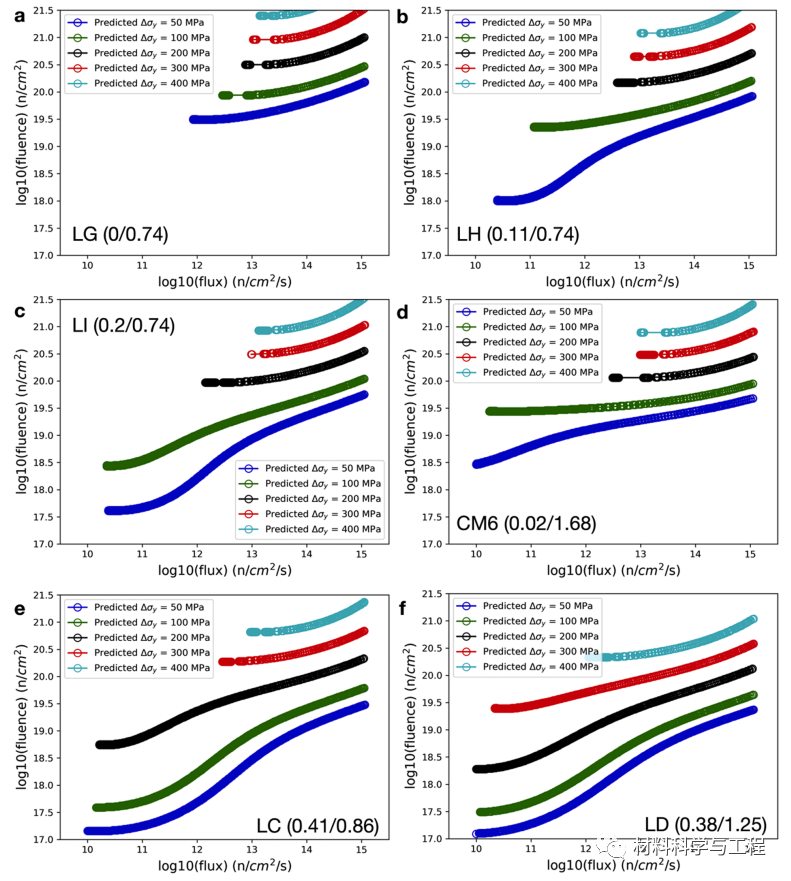
图 7. 六种核心合金的 ML 预测对数与对数辐照等淬曲线图(50 至 400 兆帕)。
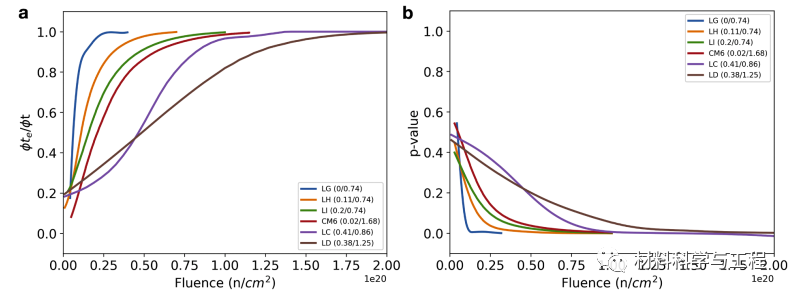
图 8:(a) 在 290 ℃ 和 1.38 × 1012 n/cm2/s条件下六种核心合金的 ML 预测 ɸte/ɸt,以及(b) 缩放 p 值 vs. 通量图。参考通量 (ɸr) 为 5 × 1010 n/cm2/s。
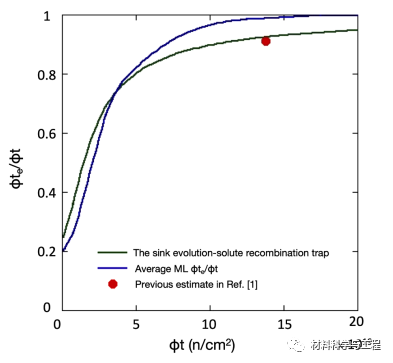
图 9. 六种核心合金的 ML 预测平均 ɸte/ɸt(蓝线)与沉演化-绝对重组陷阱模型(绿线)的比较
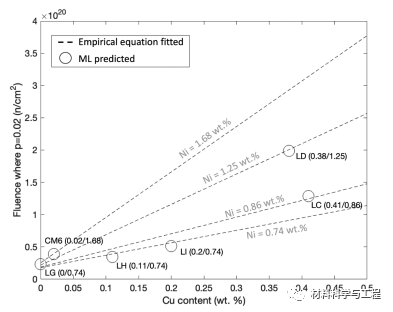
图 10. p = 0.02时的波动(ɸt0.02)与铜和镍的函数关系。
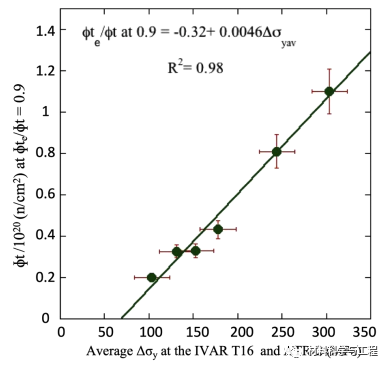
图 11. IVAR T16和 ATR-2 辐照条件下,ɸte/ɸt = 0.9 (ɸt0.9)时的通量与平均 Δσy 的函数关系。显示的 ML 预测数据数为 6。
以往的辐照效应模型通常是一种"以物理学为中心 "的自下而上的方法,它基于对辐射损伤的机理理解和相关的速率理论模型,并受制于各种假设和近似值。而 ML 则提供了另一种 "以数据为中心 "的方法,这种方法可以揭示 FLUX 效应等问题,而无需先验的机理和模型假设作为指导。这两种截然不同的方法的趋势趋同为它们提供了强有力的支持。事实上,物理方法和 ML 方法是高度互补的。此外,在本研究分析的试验反应堆数据中,对于ɸte/ɸt 的综合影响和合金成分依赖性,ML 提供了非常有用的、全新的定量见解。这不仅具有重要的实际意义,而且为正在进行的物理建模工作提供了巨大的启示。从直接实用的角度来看,这些结果也非常重要。这些结果进一步验证和反驳了我们之前的结论,即高通量、中流量的 ATR-2 数据几乎不受通量的影响,从而为 OWAY 模型提供了独立的验证。(文:SSC)
本文来自微信公众号“材料科学与工程”。欢迎转载请联系,未经许可谢绝转载至其他网站。
