机器学习包括以下步骤:
成本直觉
当大家首次使用机器进行机器学习时,会发现它的预测结果简直是糟糕透顶。
所以我们就像“给孩子纠正错题一样纠正模型,告诉它错了,但对于机器,我们更进一步——我们告诉它错在哪里,这被称为模型的“成本”。
假设我们训练一个模型来区分猫和狗,并用三张狗的照片进行测试,结果,它把所有照片都归类为猫。
它答错了3题(0/3),表现的很差,我们可以通过成本来量化错误率,基本实现方式如下:
成本 = 错误数量 / 总预测数量
因此对于我们这个超级糟糕的模型来说,在3次预测中它犯了3次错误,所以成本 = 3/3 = 1,这是模型可能达到的最高成本。
机器学习的全部目标就是尽可能降低这个成本指标,成本为0意味着在总共3次预测中没有错误预测(0/3),即模型预测全部正确。
只需记住这一点:低成本 = 好模型,高成本 = 坏模型
你可以把成本看作是成绩的同义词——如果你某门课得了D,那你可能没真正掌握这门课的内容;
但如果你得了A,那就说明你学得很棒。
我们究竟如何降低这个成本呢?这就需要用到复杂的数学了,在后面的内容我们将会学到。
现在让我们用神经网络来打个比方,顾名思义,神经网络试图模仿人脑的工作方式,以期创造出能与人类相媲美的人工智能。
人脑有1000亿个神经元,所以人脑的机器模型(即神经网络)将有1000亿个计算单元,为了简化,我们称之为参数。
如果成本是衡量模型表现有多差的指标,那么它首先需要模型的输出,而输出又需要这1000亿个参数来计算最终结果。
这使得成本成为一个庞然大物般的函数,它接收1000亿个变量,并输出一个数字。
机器学习总结
现在,你已经知道什么是机器学习了,当我们试图让机器学习模型对图像或数据等进行分类时,我们会告诉它正确答案,并在数据上对其进行测试。
通过测试,我们得到了一个衡量模型预测有多糟糕的成本指标,再通过一个涉及复杂数学的迭代过程来最小化这个成本。
当成本被最小化时,意味着模型几乎能像人类一样正确预测事物了。
矩阵速成
矩阵是表示方程组的一种简洁方式,在机器学习中,当你需要同时处理数百个数字时(这种情况经常发生),矩阵是让一切变得清晰易懂的关键。
例如,如何简洁地表示 (2 * 1) + (3 * 5) + (2 * 2) ?可以这样表示:

点积
这里,我们正在对两个向量进行一种称为点积的操作,具体步骤如下:
将第一个向量的第一个元素与第二个向量的第一个元素相乘。
将第一个向量的第二个元素与第二个向量的第二个元素相乘。
将第一个向量的第三个元素与第二个向量的第三个元素相乘。
将这三个数相加,得到的就是点积。
你按顺序将两个向量的每个元素配对,相乘,然后将这些结果相加。我们来进行一下计算:
将它们相加,得到 2 + 15 + 4 = 21,所以当两个向量进行点积时,你会得到一个单一的数字和,我们称之为标量。
请注意,如果两个向量的长度不同,则无法进行点积。
如果一个向量有2个元素,而第二个向量有3个元素会怎样?
第二个向量的第三个元素就没有其他元素可以与之配对了,这会导致计算无法进行。
向量只是一维矩阵,意味着它们就像一列数字。
矩阵则更为复杂,它们是二维的可以有很多行和列。下面是一个矩阵的例子:
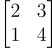
一个拥有2行2列的矩阵
让我们回顾一下术语:
当你想到标量时,就想到一个单一的数字。
当你想到向量时,就想到一列数字。
当你想到矩阵时,就想到一个数字表格。
为何我们要如此关注矩阵呢?这是因为矩阵乘法能将大量繁琐的数字运算转化为简洁的表达式。比如说,倘若我想将众多数字相乘,但我不想要一个最终的总和结果——而是希望得到一个新的矩阵,这该如何实现呢?
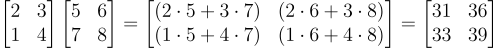
两个矩阵相乘的示例
矩阵乘法的工作原理如下:
在第一个矩阵中,取第一行(因为它是一维的,只是一列数字,所以它是一个向量)和第二个矩阵的第一列(也是一个向量!)进行点积。这就是结果矩阵的第一个元素。这是 (25 + 37) 的计算。
在第一个矩阵中,取第一行和第二个矩阵的第二列进行点积。这就是结果矩阵的第二个元素。这是 (26 + 38) 的计算。
在第一个矩阵中,取第二行和第二个矩阵的第一列进行点积。这就是结果矩阵的第三个元素。这是 (15+ 47) 的计算。
矩阵乘法就是这样既繁琐又令人困惑,但好消息是,你不必理解如何进行矩阵乘法,只需知道何时可以进行。
矩阵乘法最重要的是理解每个矩阵背后的维度以及结果矩阵的样子。
矩阵乘法的维度
如果一个矩阵有2行和2列,那么它是一个2 x 2矩阵(“x”读作“乘”)。
如果一个矩阵有3行和4列,那么它是一个3 x 4矩阵。
所以描述矩阵维度的一般公式是行 x 列,始终如此,这种表示法对于理解我们可以和不能将哪些矩阵组合相乘非常重要。
如果第一个矩阵的维度是a x b,第二个矩阵的维度是b x c,那么两个矩阵可以相乘,结果矩阵的维度将是a x c。
这是什么意思呢?第一个矩阵的列数必须与第二个矩阵的行数完全相等。
让我们尝试一个无法直接相乘的矩阵组合:
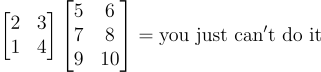
一个2×2矩阵与一个3×2矩阵无法进行矩阵乘法运算的示例
如果我们尝试对第一个矩阵的第一行和第二个矩阵的第一列进行点积,你会发现9是孤零零的,我们无法把它配对相乘
大家可能已经发现的一般规则是,第一个矩阵的行必须与第二个矩阵的列大小相同(元素数量相同),如果两个向量的大小不同,则无法进行点积。
如果我们把这两个矩阵调换位置会怎样呢?
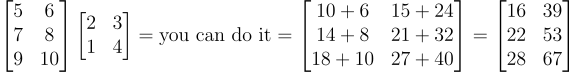
一个3×2的矩阵与一个2×2的矩阵相乘,会得到一个有效的3×2矩阵。
当前矩阵相乘时,其维度严格遵循 a×b 与 b×c 的匹配模式,最终会生成一个 a×c 的结果矩阵。下面我们结合具体维度来分析:
设定 a 为第一个矩阵的行数,这里 a = 3;
设定 b 为第一个矩阵的列数,此时 b = 2;
设定 c 为第二个矩阵的列数,可得 c = 2。
由此可见,一个 3×2 的矩阵与一个 2×2 的矩阵相乘,会得到一个 3×2 的结果矩阵,形象点说,就像是中间相同的维度“消去”了。
为了进一步巩固这个知识点,我们再来看一个例子。一个 4×8 的矩阵和一个 8×3 的矩阵相乘,最终结果矩阵的维度是 4×3。
最后一个需要注意的提示是,在相乘矩阵时,顺序很重要。
下面是一个例子,我们将两个2 x 2矩阵相乘(因此它们的维度总是有效的),但我们以两种不同的顺序进行乘法,结果却大相径庭。
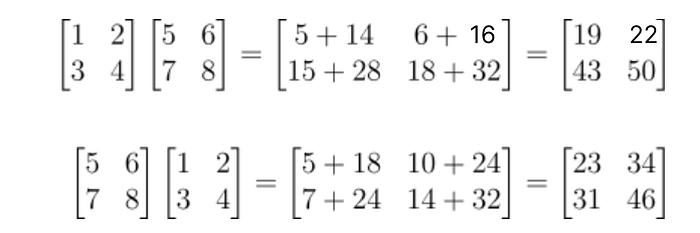
矩阵乘法不满足交换律的示例
在机器学习的背景下,矩阵相乘的顺序可能非常令人困惑,但最重要的是让维度匹配,矩阵乘法的这种非交换性质很重要,但你不必处理它。
现在我们已经知道矩阵维度是如何工作的了,在成功学习创建神经网络所需的所有线性代数知识之前,还有最后一步。
转置
转置是一个简单的概念,你只需切换矩阵的行和列来转置矩阵。
在下面的例子中,我们将一个3 x 2矩阵转置为一个2 x 3矩阵,“T”符号表示我们正在转置矩阵。
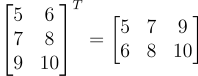
仅通过交换行和列,将一个3×2的矩阵转置为2×3矩阵的示例。
矩阵的第一列成为新转置矩阵的第一行。
矩阵的第二列成为新转置矩阵的第二行,以此类推。
为什么转置很重要呢?因为它让我们能够相乘两个原本无法相乘的矩阵。
让我们回到之前的例子:
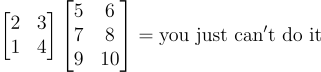
2×2矩阵与3×2矩阵相乘是不可能的。
但是如果我们将那个3 x 2矩阵转置为一个2 x 3矩阵呢?
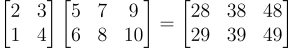
转置允许我们在不改变顺序的情况下相乘两个矩阵(之前我们就说过顺序很重要)。
根据以下定律,矩阵转置也为我们提供了矩阵乘法中的极大灵活性:
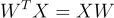
转置法则
大家可以使用下面的矩阵自己尝试证明下:
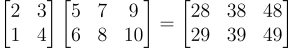
试着对这些矩阵进行乘法运算,以此验证上述法则。