彻底搞懂深度学习-向量和矩阵（动图讲解）

当你第一次听到"向量"和"矩阵"时，可能觉得它们很复杂。但如果你想真正理解深度学习，这两个概念是绕不过去的核心基础。

深度学习的本质就是数学运算，而向量和矩阵是基石。神经网络的前向传播、反向传播、梯度下降，都离不开向量和矩阵。本文将用最简单的方式，讲解它们在深度学习中的作用。

Linear Algebra for Data Science Ep1 — Introduction to Vectors and Matrices using Python | by Harshit Tyagi | TDS Archive | Medium

一、向量（Vector）

如何从深度学习的角度认识向量？

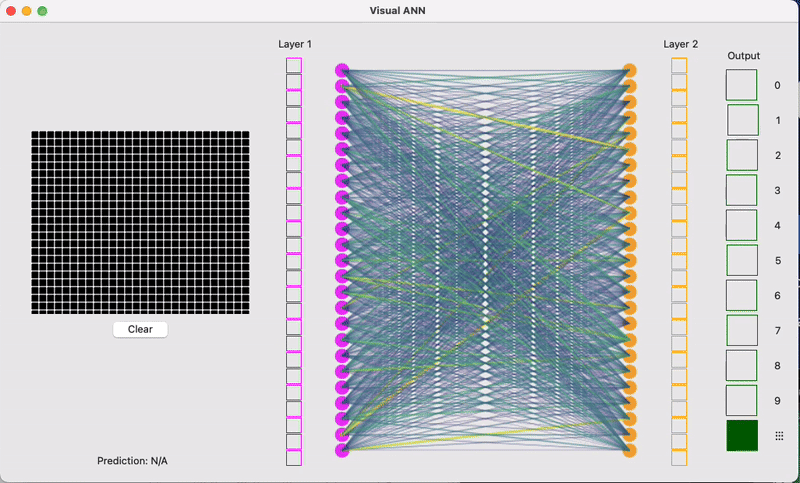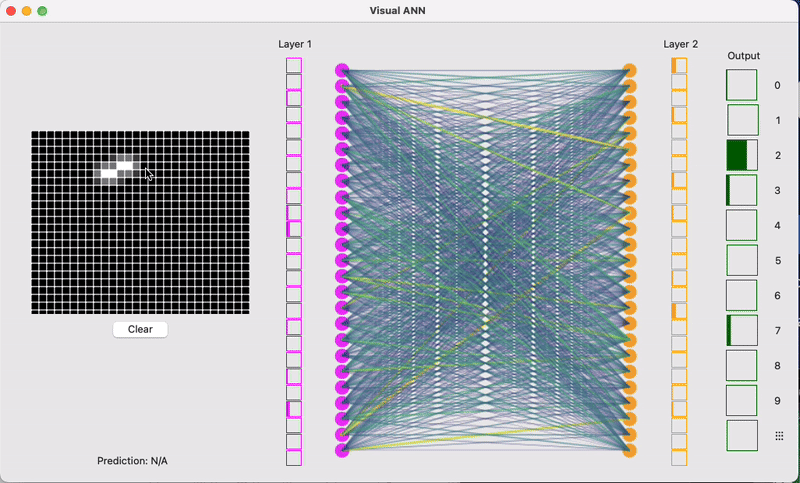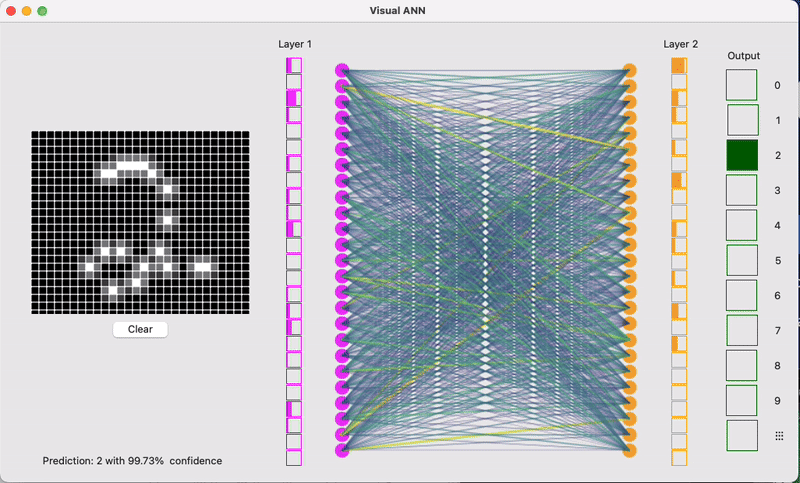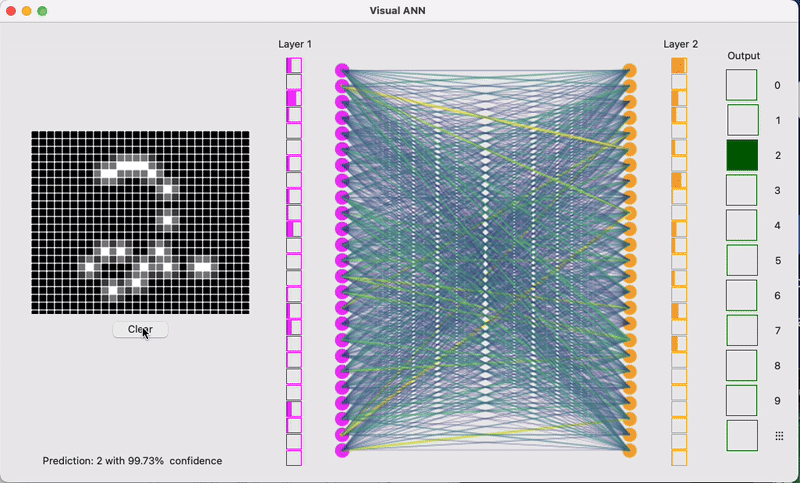
我们从一个最常见的例子开始：图像识别。假设你想训练一个CNN模型来识别手写数字，就像邮政系统自动识别邮编那样。

对于人类来说，看到一个手写的数字"8"，我们能够瞬间识别出来。但对计算机来说，它看到的不是一个数字，而是一堆像素点的集合。如果这是一张28×28像素的灰度图片，那么计算机看到的就是784个数字，每个数字代表对应像素点的灰度值（从0到255，0代表纯黑，255代表纯白）。

# 一张手写数字图片在计算机眼中的样子image_pixels = [0, 0, 0, 23, 45, 123, 200, 255, 180, 67, ...]  # 784个数字# 这就是一个784维向量，每个位置都有特定的含义

这784个有序排列的数字，就是我们说的向量。向量的本质其实很简单：它就是一组有顺序的数字。

如何理解神经网络中万物皆向量？

在AI的世界里，向量可以用统一的方式表示一切信息，即万物皆向量。

（1）数据的载体：输入都是向量

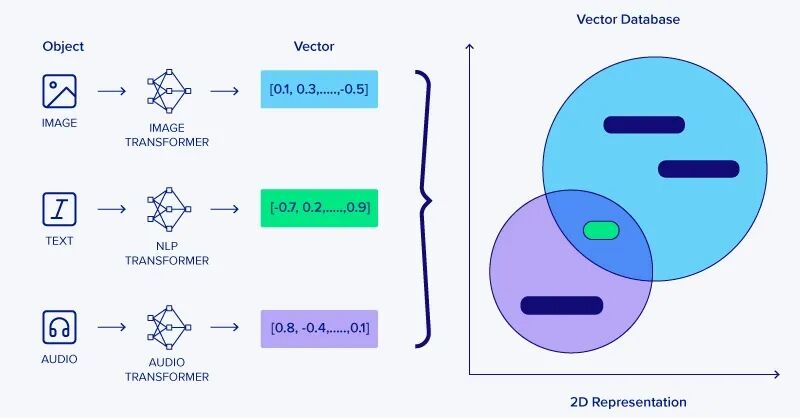
不管你处理的是什么类型的数据，在进入神经网络之前，它们都需要转换成向量的形式。从而让神经网络能够用相同的数学原理处理截然不同的数据类型。

图像数据：每张图片变成像素值向量
文本数据：每个句子变成词汇编码向量（比如"我爱机器学习"可能变成[45, 123, 67, 89]这样的数字序列）
音频数据：声音波形变成频率特征向量
结构化数据：Excel表格中的一行数据就是一个向量

Vector Database used in AI | Exxact Blog

（2）知识的存储：权重都是向量

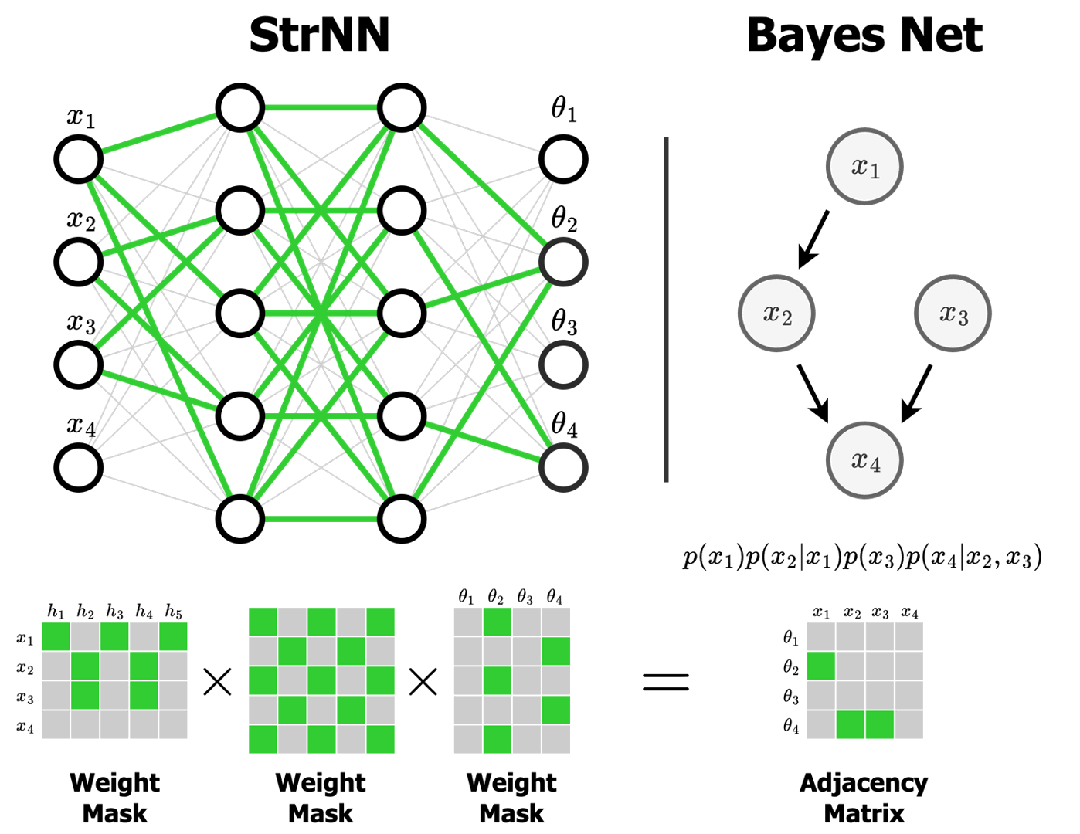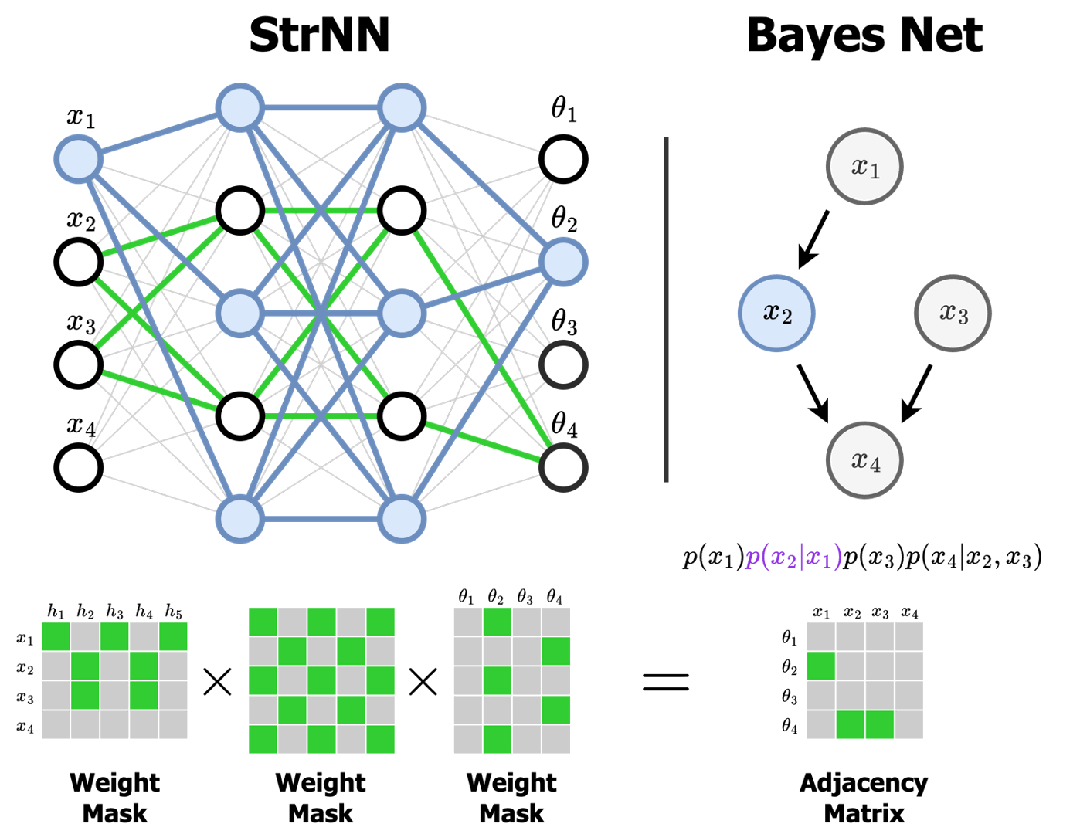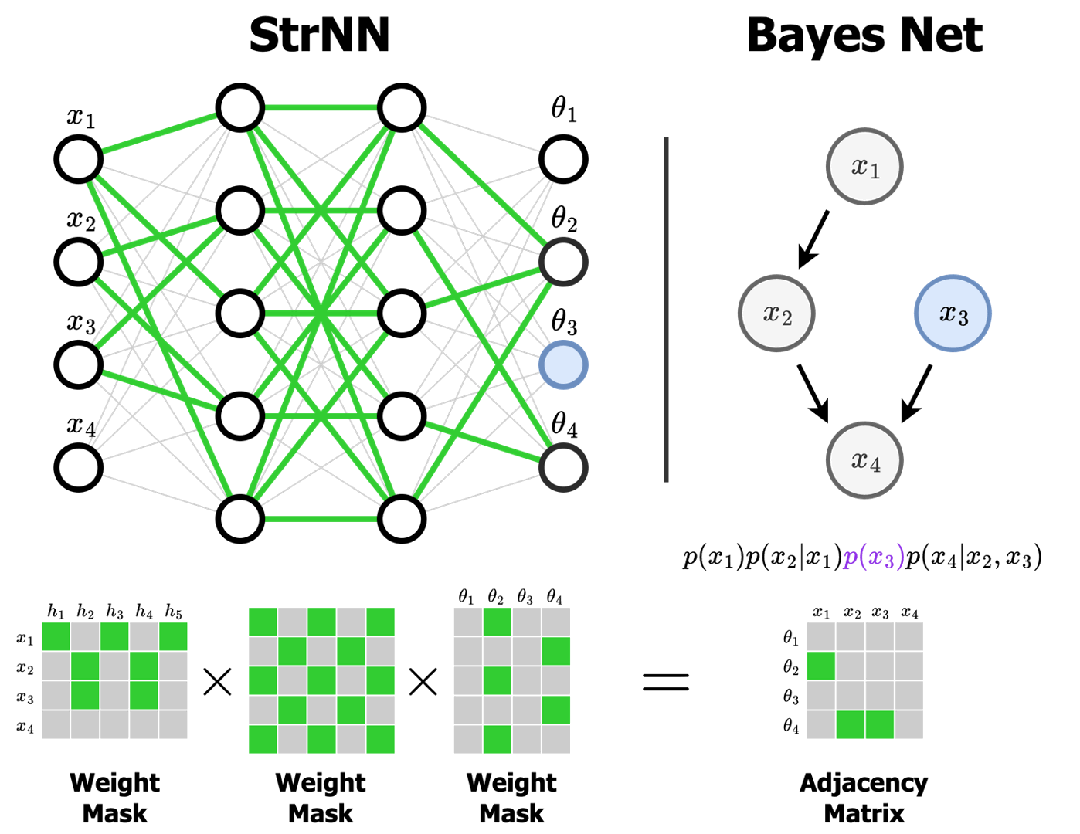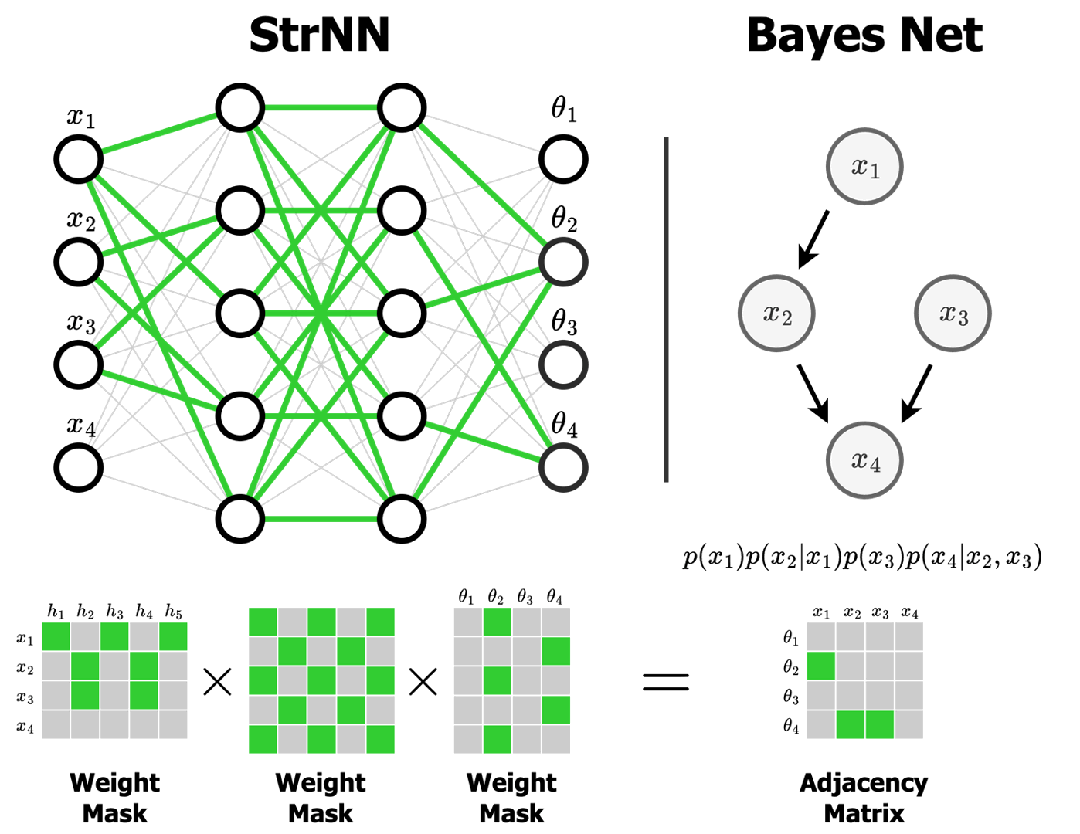
神经网络之所以"智能"，是因为它能够从大量数据中学习和记忆模式。这些学到的知识存储在哪里呢？就存储在一个个权重向量中。

# 一个简单神经元的权重向量weights = [0.3, -0.1, 0.7, 0.2, 0.8, -0.4]# 每个权重对应一个输入特征，数值大小表示重要程度# 正数表示正向影响，负数表示负向影响

（3）结果的表达：输出都是向量

神经网络的输出同样是向量形式，这个输出向量的每个元素都有特定的含义。

# 图像分类任务的输出向量（识别10种动物）output = [0.05, 0.02, 0.78, 0.01, 0.03, 0.02, 0.01, 0.06, 0.01, 0.01]#        [狗,   鸟,   猫,   鱼,   马,   牛,   羊,   兔,   猪,   鸡]# 第3个位置（猫）的概率最高，所以模型认为这是一只猫

神经网络中如何进行向量运算？

现在我们知道了向量是什么，但神经网络是如何使用这些向量进行计算的呢？答案就是点积运算。点积是深度学习中最基础、最重要的运算，它是每个神经元进行计算的核心操作。

# 输入向量（比如一张简化的3像素图片）input_vector = [1.0, 0.5, 2.0]# 权重向量（神经元学到的参数）  weight_vector = [0.3, 0.7, -0.1]# 点积计算（这就是神经元在做的事情！）result = 1.0×0.3 + 0.5×0.7 + 2.0×(-0.1)        = 0.3 + 0.35 - 0.2        = 0.45

神经网络的"智能"就来自于学会给不同输入分配合适的权重，然后做加权求和。向量点积运算就是这个加权求和过程——让每个输入乘以权重，全部加起来。这个简单运算重复千万次，就产生了人工智能。

如何通过向量相似度理解数据之间的关系？

在深度学习中，我们经常需要判断两个向量有多相似，这在推荐系统、文本分析、图像搜索等应用中极其重要。最常用的相似度计算方法是余弦相似度，它就是测量两个向量之间夹角的余弦值。

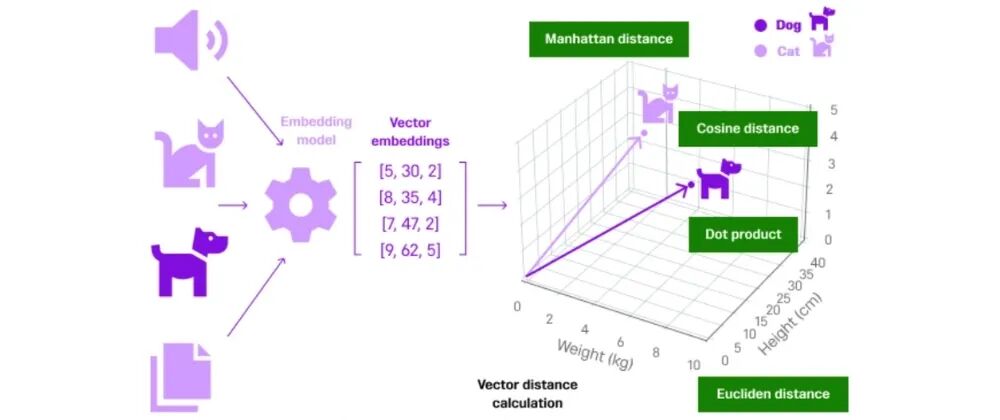
What is Vector Similarity Search? - DEV Community

夹角为0度（完全同向）：余弦值为1，表示完全相似
夹角为90度（垂直）：余弦值为0，表示无关
夹角为180度（完全反向）：余弦值为-1，表示完全相反

import mathdef cosine_similarity(vector1, vector2):    # 计算点积    dot_product = sum(a * b for a, b in zip(vector1, vector2))    # 计算向量长度    length1 = math.sqrt(sum(a * a for a in vector1))    length2 = math.sqrt(sum(a * a for a in vector2))    # 计算余弦相似度    similarity = dot_product / (length1 * length2)    return similarity# 示例：比较两个用户的电影偏好user1_preferences = [5, 1, 3, 


    
4, 2]  # 对5部电影的评分user2_preferences = [4, 2, 3, 5, 1]  similarity = cosine_similarity(user1_preferences, user2_preferences)print(f"用户相似度: {similarity:.3f}")

二、矩阵（Matrix）

如何从神经网络层理解矩阵？

如果你已经理解了向量，那么理解矩阵就变得容易多了。简单来说，矩阵就是多个向量排列组合。

让我们回到神经网络的例子。之前我们看到一个神经元如何处理输入向量，但实际的神经网络层通常包含很多个神经元。比如说，一个隐藏层可能有128个神经元，每个神经元都有自己的权重向量。

# 输入：4个特征的一个数据样本input_vector = [1.0, 0.5, 2.0, 1.5]# 权重矩阵：3个神经元×4个输入特征weight_matrix = [    [0.1, 0.2, -0.3, 0.4],  # 神经元1的权重    [0.5, -0.1, 0.2, 0.8],  # 神经元2的权重    [0.3, 0.6, -0.2, 0.1]   # 神经元3的权重]# 矩阵乘法的计算过程：# 神经元1的输出 = 1.0×0.1 + 0.5×0.2 + 2.0×(-0.3) + 1.5×0.4 = 0.3# 神经元2的输出 = 1.0×0.5 + 0.5×(-0.1) + 2.0×0.2 + 1.5×0.8 = 1.85  # 神经元3的输出 = 1.0×0.3 + 0.5×0.6 + 2.0×(-0.2) + 1.5×0.1 = 0.18layer_output = [0.3, 1.85, 0.18]

这样，整个神经网络层的所有权重就形成了一个矩阵。矩阵的每一行代表一个神经元的权重，每一列代表所有神经元对某个特定输入特征的权重分配。

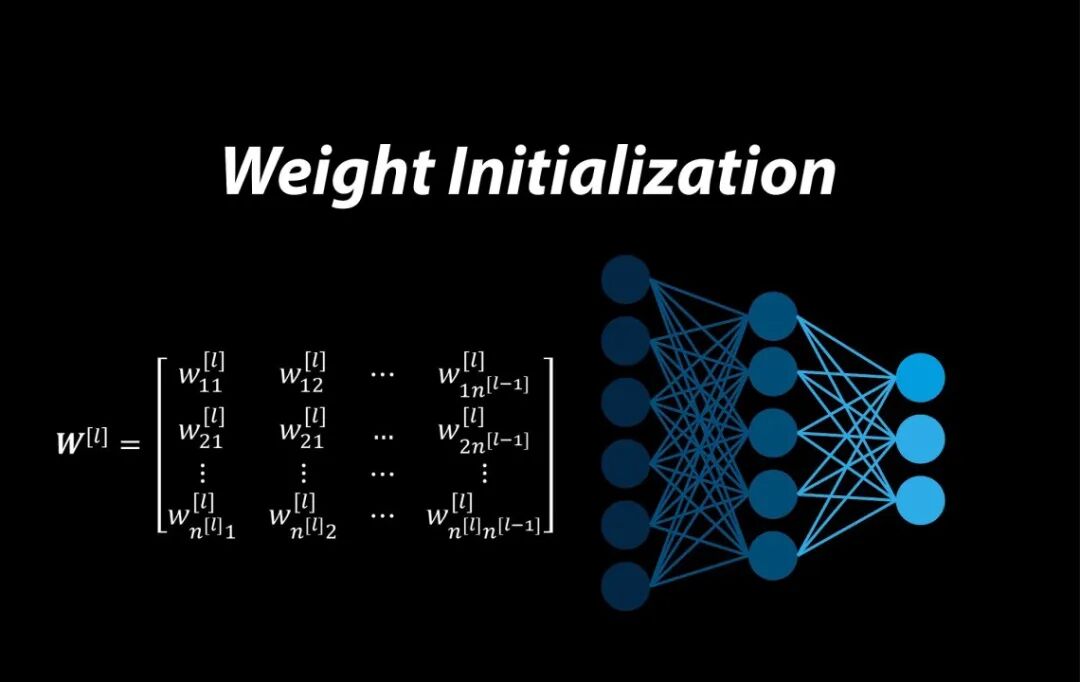
Review on initializing Neural Network with Random Weights

如何通过矩阵乘法让神经网络的"魔法变换"？

现在我们来到到最关键的部分：矩阵乘法。这个运算看起来可能有些复杂，但它实际上就是把我们之前学过的点积运算批量化执行。

# 输入：4个特征的一个数据样本input_vector = [1.0, 0.5, 2.0, 1.5]# 权重矩阵：3个神经元×4个输入特征weight_matrix = [


    
    [0.1, 0.2, -0.3, 0.4],  # 神经元1的权重    [0.5, -0.1, 0.2, 0.8],  # 神经元2的权重    [0.3, 0.6, -0.2, 0.1]   # 神经元3的权重]# 矩阵乘法的计算过程：# 神经元1的输出 = 1.0×0.1 + 0.5×0.2 + 2.0×(-0.3) + 1.5×0.4 = 0.3# 神经元2的输出 = 1.0×0.5 + 0.5×(-0.1) + 2.0×0.2 + 1.5×0.8 = 1.85  # 神经元3的输出 = 1.0×0.3 + 0.5×0.6 + 2.0×(-0.2) + 1.5×0.1 = 0.18layer_output = [0.3, 1.85, 0.18]

矩阵乘法让我们能够同时计算多个神经元的输出！ 所有神经元的计算可以并行进行，这大大提升了计算效率。

通过这篇文章，你应该理解了向量和矩阵在深度学习中的核心作用：深度学习就是让输入数据（向量）通过一系列变换（矩阵乘法），逐步提取特征，得到最终结果。过程虽然复杂，但数学原理很简单。

日拱一卒，让大脑不断构建深度学习和大模型的神经网络连接。