阅读大概需要5分钟
跟随小博主,每天进步一丢丢

昨天详细谈了谈最简单的SVM,相比较于今天要讲的Soft Margin SVM来说,昨天讲的其实是Hard Margin SVM,没看过的朋友们可以点击这里:
【机器学习】今天想跟大家聊聊SVM
还是举一个例子吧
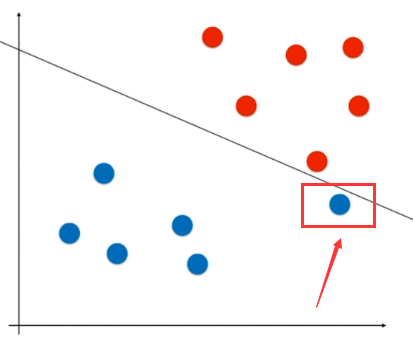
该点属于蓝色类别,所以决策线如图所示。但是这个决策边界如果运用到现实环境中的话,肯定会有很大的误分类点。也就是该分类线没有泛化能力。关于上述的情况,其实我们的理想分类线应该为:
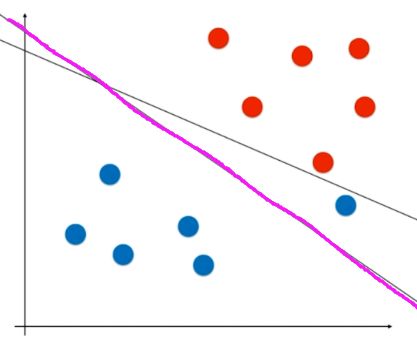
虽然在训练集中分类效果不好,但是它具有一定的泛化能力!毕竟我们的模型最终都是要用到现实生活中去的。
再比如存在线性不可分的点,但还是理想情况还是可以分的情况,如
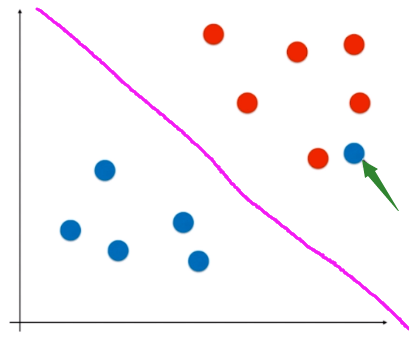
而能解决上述2种问题的SVM就被成为Soft Margin SVM,允许一些点进行错误分类。
我们先回顾下之前的SVM(Hard Margin SVM)的优化公式:
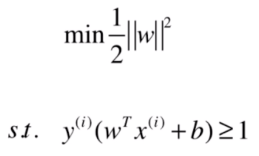
像上述距离的两种情况不能分类的具体原因就是该条件的限制:
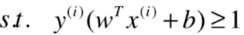
现在我们允许一些点犯错,也就是允许一些点不满足这个公式,放放水,所以对每个点引入一个松弛变量(大于等于0),使得
 +它的松弛变量 >= 1
+它的松弛变量 >= 1
即可,转换下公式为
 >= 1 - 它的松弛变量
>= 1 - 它的松弛变量
上述式子的专业公式为:
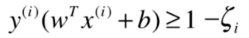
但是松弛变量也不能太大,得需要有东西看着它,怎么看着呢?当然就是用目标函数啦。又因为每个数据点都有自己的松弛变量,所以需要需要求和作为最终目标函数的一部分:
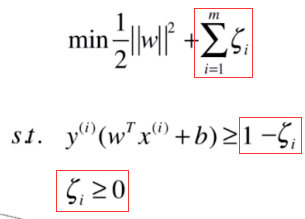
但是这样的目标函数
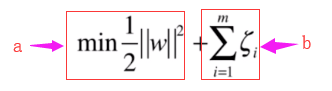
表示a和b重要性是相同的。但是实际上a,b是有各自的权重的,但是这里其实只要在b部分加个权重C即可:
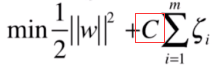
当C越大时,代表主要是优化b部分,所以就对于b项很严格,最终就使得结果越接近Hard Margin SVM。反之,当C越小时,代表主要优化a部分,就对于b宽松很多,最终就是的结果非常的Soft Margin SVM。如何选择C值,自己调试即可。
所以最终的完整目标函数为:
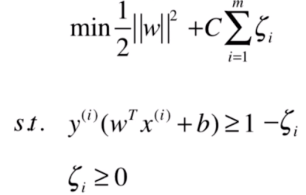
正则化,听起来有难度的赶脚,但是实际上很简单,比如上述的目标函数就是L1正则:

这里的L1正则说的是松弛变量的幂。那样这样就很好理解L2正则啦:

常用的是L2正则,个人觉得是实验效果决定的结果吧。
这里用的是sklearn来实践的
数据介绍
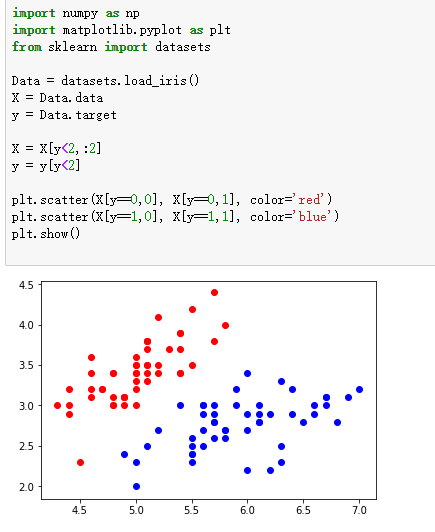
初始化SVM C = 1e9

SVM还有很多参数,感兴趣的可以自行了解哈。
可视化
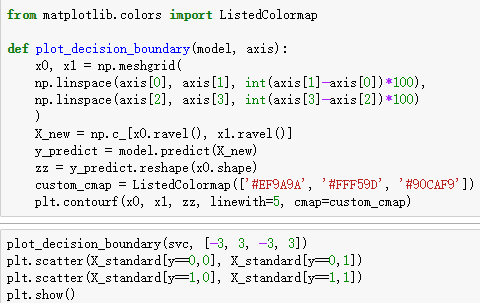
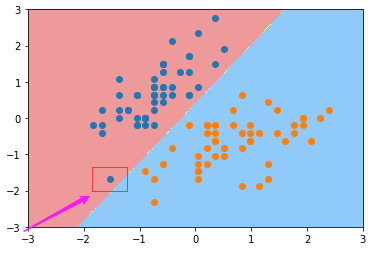
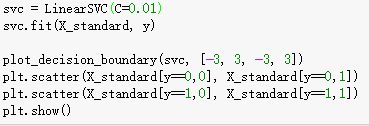
改变C的值,C = 0.01
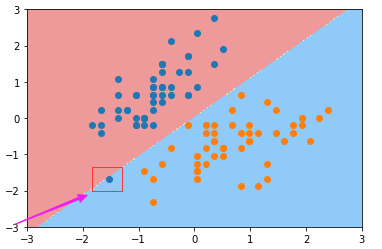
注意到该点的分类变化。
PS:今天就到这里吧,下次会带来对偶问题和核函数,以及SVM的回归模型。敬请期待!
documentation n. 文件,证明文件,史实,文件编制
clientele n. 客户;诉讼委托人
sequential adj. 连续的;相继的;有顺序的
conclusive adj. 决定性的;最后的;确定的;确实的;确定性的
introspection n. 内省;反省
推荐阅读:
一大批历史精彩文章啦
【收藏版】长文详解基于并行计算的条件随机场
【珍藏版】长文详解python正则表达式
这些神经网络调参细节,你都了解了吗
谈谈我在自然语言处理入门的一些个人拙见
大数定律和中心极限定理的区别和联系
深度学习之卷积神经网络CNN理论与实践详解
深度学习之RNN、LSTM及正向反向传播原理
TreeLSTM Sentiment Classification
基于attention的seq2seq机器翻译实践详解
【干货】基于注意力机制的seq2seq网络
欢迎关注深度学习自然语言处理公众号,我会每天更新自己在机器学习,
深度学习,NLP,linux,python以及各种数学知识学习的一点一滴!再小的人也有自己的品牌!期待和你一起进步!

点个赞呗