LMN，Python中文社区专栏作者
博客：jianshu.com/u/8a1902e9300f
事情是这样的，我最近在研究团队编组及内部模式对发挥团队能力的影响，以及如何正确编组让团队能力发挥实现最大化，别问我为什么研究这个，反正稀里糊涂就研究上了。我发现在描述团队编组间及内部同步能力的时候，人们对Kuramoto模型（藏本模型）作了大量的研究,其中包括模型达到完全相位同步的充分条件、耦合强度对于同步的影响、一定条件下振子的收敛速率等。但具体实现一般都在MATLAB中，且网上代码过于复杂（我运行了一遍一堆报错），这里我使用Python和MATLAB对Kuramoto模型简单模拟。模拟的话还是一遍举个栗子，边分析边测试效果最好，百度学术上有一篇关于Kuramoto模型的简单论文，我们就用它来实现模拟。空间信息支援力量编组模式分析，上链接:
http://xueshu.baidu.com/usercenter/paper/show?paperid=11b7c2ef69b3ac7f6e114afeb75f8083&site=xueshu_se
好吧，那我们开始，首先是Python实现。N维Kuramoto模型的数学描述如下：
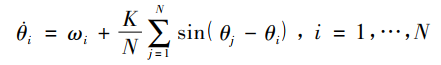
没错，是讨厌的数学公式，没事，它可以改写成这样：
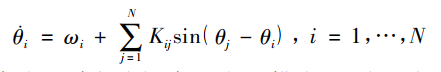
好像还是有点长，那我们在改写一下：
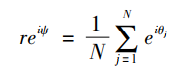
看着好多了，那我就来说说式子中参数的意义，Kij为耦合矩阵，是为了便于描述不同振子间耦合程度不同的情形。最下面那个式子的r就是我们的目标，反应振子间的相关性，这个相关性就可以描述我们想要的编组内部同步能力。
哎呦，这个式子看起来好简单，这里要补充一下知识点：同步能力可不是一下子各组该怎么同步直接确定的了，它是一个从开始到稳定的阶段，也就是说随时间变化，最终反映在各组的同步能力才会确定，那么最后图像是什么样子才算同步能力好呢？
同步能力好，是指随着时间的推移，各组的同步能力r逐渐稳定，波动现象消失或固定在某一个小范围内。需要注意的是这和各组r值之间的差距没有关系，我们要的是一个平稳的状态。那怎么办找r和t的关系呢？
注意看最上面那两个式子，相位（第一项，等号左边那个）上面有个点，这样他可就不简简单单是个相位了，它代表的是相位的变化值，是一个微小的微分值，好吧具体意思就是，那个式子左边展开之后是这样的：
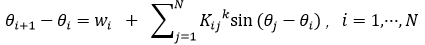
哎呀，t出现了，其实
与t有关，这里你可能有点绕，因为它们之间的关系是一一对应的，就是说每个时间的t对应了一个，我下面带入具体数值的时候你就知道了。
组间同步能力与时间t的关系出现了！
也就是说我先用上面的那个公式4计算出来的值，在带入到公式5，那么t-r关系就可以明确下来了，那现在我们再回过头来看看文章中已经给的例子，看看还有没有未知量。
栗子是这样的栗子：
假设某机构内部有 4 个编组，每个编组包括 5 个节点(其中 1 个节点为领导节点) 。另外，将上级领导作为一个独立的编组，且只包含一个节点。假设在领导机关增加4名信息传递人员。当以独立编组模式编组时，指定1名信息传递人员为指挥者，其指挥关系与其他编组一致; 当分散编组时，信息传递力量节点的关系与所在编组其他节点指挥关系一 致。其中，完全分散编组模式时，各信息传递力量节点之间无信息共享通道; 不完全分散编组时，在各信息传递人员节点之间建立一条信息共享通道。各编组模式及其拓扑结构如下图所示：
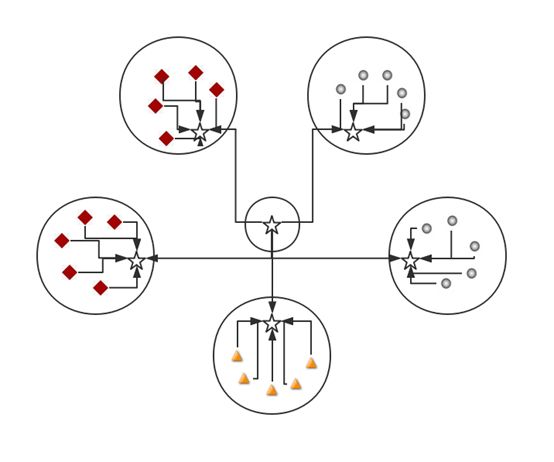
独立编组模式
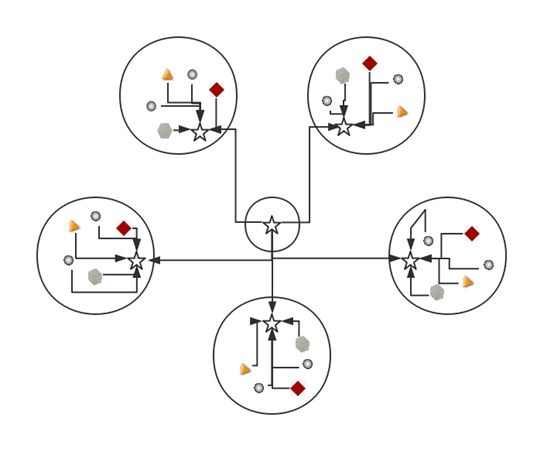
完全分散编组
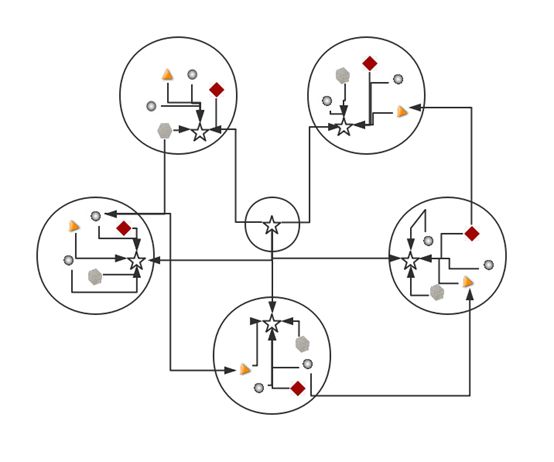
不完全分散编组
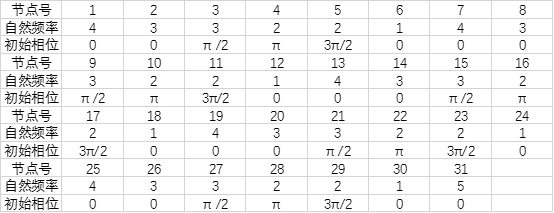
参数数据
参数确定一下有没有未知量：
首先N，数据数目已知，这个有了。
K值是分组内的连接强度，这个是看实际情况，由甲方提供或者自己看着给的，这里就是甲方给的编组图，i与j点的链接强度一目了然，这个有了。
是振子i的固有频率，也称自然频率，甲方会给，没法自己估计，这个有了。
怎么办，初始的会给，自己也能测的出来，但那么多
得多少不知道啊，这里通过翻看文章，我发现其实文章是有一个特殊条件的，不然的话是需要研究耦合因子求三种约束条件解情况的，特殊条件就在这：
假设编组内节点的初始相位差为π/2，且编号最小者为0，随编号增大而增大。
哦，初始相位差知道了，你还告诉了我各个初始相位，那么的值就在一个范围内的几个固定值里面啊！
好的，没有未知量了，就是找K的时候麻烦点，没办法，这个决定了编组的不同，写脚本算一下吧：
#codingutf-8
##ScriptName:KuramotoSimulation.py
import matplotlib.pyplot as plt
from
pylab import
from sympy import
from matplotlib.ticker import MultipleLocator, FormatStrFormatter
import math
import numpy as np
N = 31 #总节点数
c=[0,0,math.pi 2,math.pi,3 math.pi 2,0,0,0,math.pi 2,math.pi,3 math.pi 2,0,0,0,math.pi 2,math.pi,3 math.pi 2,0,0,0,math.pi 2,math.pi,3 math.pi 2,0,0,0,math.pi 2,math.pi,3 math.pi 2,0,0]
w = [4,3,3,2,2,1
,4,3,3,2,2,1,4,3,3,2,2,1,4,3,3,2,2,1,4,3,3,2,2,1,5]
k1 = [
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2],
[1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[1,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[1,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,1,0.9,0.9,0.9,0.9,0.9,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,2],
[0,0,0,0,0,0,0.9,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0.9,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0.9,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0.9,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0.9,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,1,0.8,0.8,0.8,0.8,0.8,0,0,0,0,0,0,0,0,0,0,0,0,2],
[0,0,0,0,0,0,0,0,0,0,0,0,0.8,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0.8,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0.8,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0.8,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0.8,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0.7,0.7,0.7,0.7,0.7,0,0,0,0,0,0,2],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.7,1,0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.7,0,1,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.7,0,0,1,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.7,0,0,0,1,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.7,0,0,0,0,1,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,0.6,0.6,0.6,0.6,0.6,2],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.6,1,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.6,0,1,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.6,0,0,1,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.6,0,0,0,1,0,0],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.6,0,0,0,0,1,0],
[2,0,0,0,0,0,2,0,0,0,0,0,2,0,0,0,0,0,2,0,0,0,0,0,2,0,0,0,0,0,1]]
n = [i + 1 for i in range
(22)] #目标划分,24个值,1-24
t = [j for j in range(1000)]
ci = 0
C = []
C.append(c)
for d in range(1100)
for i in n
for j in range(22)
cj = c[j + 1] - c[i]
ci += k1[i][j + 1] math.sin(cj)
cii = ci + w[i]
h = [0.01 cii + z for z in c]
C.append(h)
c = h
def r_function(u)
y1 = 0
y2 = 0
y12 = 0
y22 = 0
r = []
for x in range(1000)
for ul in u
y1 += math.cos(C[x][ul])
y2 += math.sin(C[x][ul])
y12 = y1 2
y22 = y2 2
r.append((float(1) N ) ((y12 + y22) 0.5))
return r
r1 = r_function([1,2,3,4,5,6])
r2 = r_function([7,8,9,10,11,12])
r3 = r_function([13,14,15,16,17,18])
r4 = r_function([19,20,21,22
,23,24])
r5 = r_function([25,26,27,28,29,30])
#r6 = r_function([31])
ax = subplot(111) #注意一般都在ax中设置,不再plot中设置
ymajorLocator = MultipleLocator(0.1) #将y轴主刻度标签设置为0.5的倍数
ax.yaxis.set_major_locator(ymajorLocator)
plt.plot(t, r1, marker='o', color='green', label='1')
plt.plot(t, r2, marker='D',color='red', label='2')
plt.plot(t, r3, marker='+',color='skyblue', label='3')
plt.plot(t, r4, marker='h', color='blue', label='4')
plt.plot(t, r5, marker='_',color='yellow', label='5')
#plt.plot(t, r6, color='red', label='6')
plt.legend() # 显示图例
plt.xlabel('iteration times')
plt.ylabel('r')
plt.show()
独立编组结果如图：
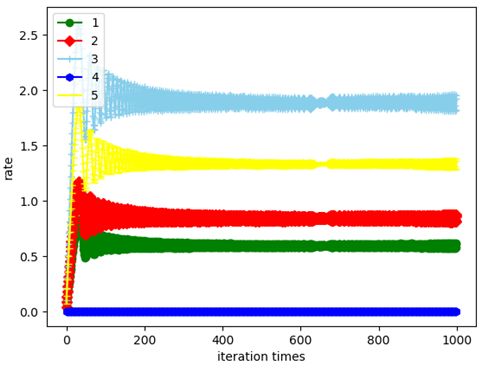
k1独立编组
好的，从图像我们来看看Kuramoto模型在描述这个编组的时候，5组最终稳定，我们说这个团队编组还算科学，但我们改变一下K的值，换成分散编组：
k2 = [[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [1,1,0.9,0.8,0.7,0.6,0,0,0,0,0,0,0,0,0,0
,0,0,0,0,0,0,0,0,2], [1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [0.9,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,0], [0.8,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [0.7,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0
,0,0,0,0,0,0,0,0], [0.6,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [0,0,0,0,0,0,1,1,0.9,0.8,0.7,0.6,0,0,0,0,0
,0,0,0,0,0,0,2], [0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [0,0,0,0,0,0,0.9,0,1,0,0,0,0,0,0,0,0,0,0
,0,0,0,0,0,0], [0,0,0,0,0,0,0.8,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], [0,0,0,0,0,0,0.7,0,0,0,1,0,0,0,0,0,0,0,0
,0,0,0,0,0,0], [0,0,0,0,0,0,0.6,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,1,0.9,0.8,0.7,0.6,0,0,0
,0,0,0,2], [0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0,0,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0.9,0,1,0,0,0,0,0,0
,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0.8,0,0,1,0,0,0,0,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0.7,0,0,0,1,0,0,0,0,0,0
,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0.6,0,0,0,0,1,0,0,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0.9
,0.8,0.7,0.6,2], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,0,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
,0.9,0,1,0,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.8,0,0,1,0,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0
,0,0,0,0,0.7,0,0,0,1,0,0], [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.6,0,0,0,0,1,0], [2,0,0,0,0,0,2,0,0,0,0,0
,2,0,0,0,0,0,2,0,0,0,0,0,1]
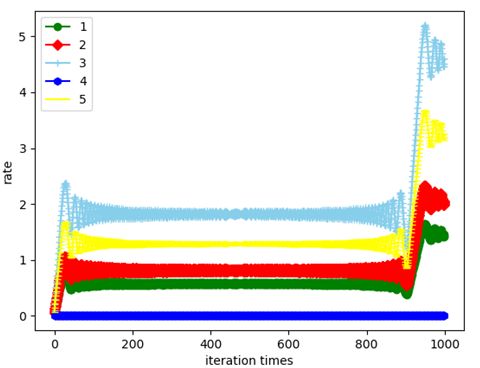
k2独立编组
这两幅图像都在开始阶段大幅波动，而后在一定范围内趋于稳定，那么到底哪个分组模式最符合实际，最能突出编组能力呢？
这里还有一个公式，来解决这个问题，编组同步能力的量化：
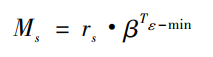
就可以描述某编组的同步效果，
是达到稳定状态后序参量的均值，β∈(0,1)是调节因子。我们可以用
比较编组内部的好坏。那编组间能力的好坏怎样比较呢？
这个Kuramoto模型同样有所考虑，它有一个描述整个系统编组能力的公式：
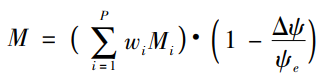
其中，P是编组的数量，
是第i个编组的同步能力，
是编组在整个系统中的权重，
是各编组平均 相位的均值，
是各编组平均相位的标准差。具体的计算不是这篇文章的重点，就不再计算
和M的值来比较上述例子独立编组和分散编组的好坏了，本篇文章主要是讲下Kuramoto模型的解决思路，尤其是上面解决
值的方法可以套用在其他Kuramoto模型中，做一个目标估计绰绰有余的。
文章能看到最后真的很不容易，代码及对数据的延伸都已上传至GitHub和Gitee上，求star：
GitHub：https://github.com/wangwei39120157028/Spatial_Information_Support_Force_Grouping_Mode_Analysis
Gitee：https://gitee.com/wwy2018/Spatial_Information_Support_Force_Grouping_Mode_Analysis
▼ 点击成为社区注册会员 「在看」一下，一起PY！
