在前面两节有关向量内容的基础上，这一小节里我们开始接触矩阵的相关概念。矩阵应该说是线性代数这门学科中出现率最高频的词汇了，他可以被看作是排列的向量或者是堆放在一起的数字。矩阵的意义非常重要，他可以作用在一个具体的向量上，使其空间位置发生变换。
在本节的内容中，我们会逐步学习到矩阵的基本运算规则，了解如何通过矩阵的作用改变向量的空间位置，并使用Python语言工具对其运算过程进行描述。与此同时，我们还会看到一些具有特殊形态的矩阵，也许这些特殊矩阵从表面看上去概念很简单，但是他们在后面章节的内容介绍中，都会分别扮演非常重要的角色，希望读者能细细体会，筑牢知识基础。
介绍完了向量基本概念，这一节我们开始介绍矩阵。对于矩阵而言，最直观的描述就是一个m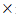
n的数字方阵。他可以看作是n个m维列向量从左到右并排摆放，也可以看成是m个n维行向量从上到下进行叠放。
我们举一个例子来看看：有一个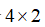
的矩阵
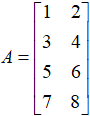，显而易见，他由4行2列构成，一共包含8个元素，每一个元素都对应矩阵中的一个数据项，例如，第一行第二列的项是2，我们也可以将其表示为
。
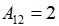那如果我们想使用Python语言来表示上面这个矩阵，也是非常简单的。我们可以使用numpy中的二维嵌套数组来完成这项任务。
代码如下：
import numpy as np
A = np.array([[1, 2],
[3, 4],
[5, 6],
[7, 8]])
print(A)
print(A.shape)
运行结果：
[[1 2]
[3 4]
[5 6]
[7 8]]
(4, 2)
我们着重强调一下，在形容矩阵的形状和规模的时候，一般采用其行数和列数来进行描述。对应到代码中，我们通过矩阵A的shape属性，就可以获取一个表示规模的元组对象，这个元组对象包含两个元素：第一个元素表示行数，第二个元素表示列数。从结果中我们可以看出，这个矩阵拥有4行2列。
在上文中，我们刚刚初步接触了一个规模为4×2矩阵，这个矩阵非常的普通，这里我们再补充一些特殊形态的矩阵，这些矩阵的特殊性不光体现在外观形状上，更在后续的矩阵实际应用中发挥重要的作用。
1.方阵
对于行数和列数相等的一类矩阵，我们称之为方阵，其行数或列数称之为他的阶数。下面我们看到的就是一个4阶方阵：
。我们用Python语言来表示这个方阵，并观察他的阶数。
代码1-15：
代码片段
import numpy as np
A = np.array([[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3],
[4, 4, 4, 4]])
print(A)
print(A.shape)
运行结果
[[1 1 1 1]
[2 2 2 2]
[3 3 3 3]
[4 4 4 4]]
(4, 4)
2.转置与对称矩阵
在开始介绍对称矩阵之前，我们先来说一下矩阵转置的有关概念。对于指定的矩阵
，如果我们将其行和列上的元素进行位置互换，就可以得到一个全新的矩阵：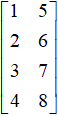
。这里，我们就把这个新矩阵称之为原矩阵A的转置矩阵，记作：
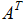，行和列互换的矩阵操作就称之为矩阵的转置。
代码如下：
import numpy as np
A = np.array([[1, 2, 3, 4],
[5, 6, 7, 8]])
print(A)
print(A.T)
运行结果：
[[1 2 3 4]
[5 6 7 8]]
[[1 5]
[2 6]
[3 7]
[4 8]]
如果原矩阵和转置后新得到的矩阵相等，那么这个矩阵我们就把他称作是对称矩阵。由此可见，矩阵对称的前提条件首先必须得是一个方阵；其次，在方阵S中的每一项元素，都必须满足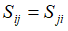
的相等关系。
我们举一个实际例子来看看，例如矩阵：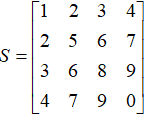
代码如下：
import numpy as np
S = np.array([[1, 2, 3, 4],
[2, 5, 6, 7],
[3, 6, 8, 9],
[4, 7, 9, 0]])
print(S)
print(S.T)
运行结果：
[[1 2 3 4]
[2 5 6 7]
[3 6 8 9]
[4 7 9 0]]
[[1 2 3 4]
[2 5 6 7]
[3 6 8 9]
[4 7 9 0]]
在对阵矩阵中我们不难归纳出一个典型的特征，即：沿着从左上到右下的对角线，关于这条对角线相互对称的元素都是彼此相等的。在后面的内容中你会不断的发现：如果我们将对称矩阵称之为最重要的矩阵，是丝毫不为过的。他在矩阵的相关分析中会扮演极其重要的角色。
3.零矩阵
顾名思义，对于所有元素都等于0的矩阵，我们将其称之为零矩阵，记作O。我们还可以通过下角标来描述矩阵的规模，像下面这个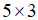
的零矩阵
，我们可以将其记作是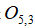
。
代码如下：
import numpy as np
A = np.zeros([5, 3])
print(A)
运行结果：
[[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]]
4.对角矩阵
还有一种特殊的方阵，在他的非对角线位置上矩阵的元素全部都为0，我们将这种矩阵称之为对角矩阵，例如：
，0元素的位置我们可以省去不写。在Python语言中，有一种更为简便的方法来生成一个对角矩阵：
代码如下：
import numpy as np
A = np.diag([1, 2, 3, 4, 5])
print(A)
运行结果：
[[1 0 0 0 0]
[0 2 0 0 0]
[0 0 3 0 0]
[0 0 0 4 0]
[0 0 0 0 5]]
5.单位矩阵
单位矩阵并不指的是所有元素都为1的矩阵，而是指对角位置上元素均为1，其余位置元素均为0的特殊对角矩阵。n阶单位矩阵记作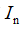
，下面我们用Python工具来生成一个5阶单位矩阵：
。
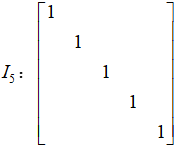代码如下：
import numpy as np
I = np.eye(5)
print(I)
运行结果：
[[ 1. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0.]
[ 0. 0. 1. 0. 0.]
[ 0. 0. 0. 1. 0.]
[ 0. 0. 0. 0. 1.]]
前面在介绍如何利用Python工具简单的描述一个列向量的时候，我们曾经提到过这个概念。现在介绍了矩阵，我们对此再着重的回顾一下：n维的行向量可以看作是一个1×n形状大小的特殊矩阵，而同理，n维的列向量也同样可以看作是一个n×1形状大小的特殊矩阵。
那么，这样做的目的又是什么呢？一方面，这么做可以将矩阵和向量的Python表示方法统一起来，而另一方面，在马上要介绍的矩阵与向量的乘法运算中，我们也可以将其看作是矩阵与矩阵乘法的一种特殊形式，将运算方式进行统一。
下面，我们再次从这个视角出发，利用Python工具去重新生成一个4维行向量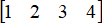
和对应的列向量
。
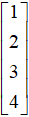代码如下：
import numpy as np
p = np.array([[1, 2, 3, 4]])
print(p)
print(p.T)
运行结果：
[[1 2 3 4]]
[[1]
[2]
[3]
[4]]
我们用生成矩阵的方法生成了一个1×4形状大小的矩阵，用他来表示一个4维的行向量。随后将其进行转置（因为是矩阵形式，所以可以运用转置方法），就得到了对应的4维列向量。
矩阵之间的加法运算必须运用到相等规模的两个矩阵之间，即：行数和列数相等的两个矩阵之间才能做加法运算。
这个道理其实非常容易理解，因为我们需要将参与加法运算的两个矩阵对应位置上的元素分别进行相加，才能得到最终的结果矩阵。
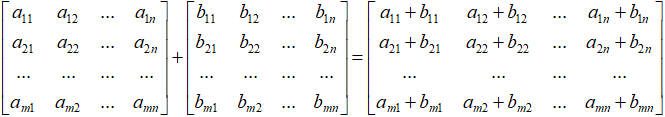
接下来，我们还是来看看实现矩阵相加的Python示例代码。求解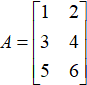矩阵
和矩阵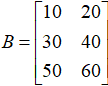
的加法运算结果。
代码如下：
import numpy as np
A = np.array([[1, 2],
[3, 4],
[5, 6]])
B = np.array([[10, 20],
[30, 40],
[50, 60]])
print(A+B)
运行结果：
[[11 22]
[33 44]
[55 66]]
矩阵的数量乘法运算描述起来也非常简单，就是将参与运算的标量数字分别与矩阵的每一个元素分别相乘，得到结果矩阵对应的新元素。所以很显然，得到的结果矩阵的大小规模也是不变的。
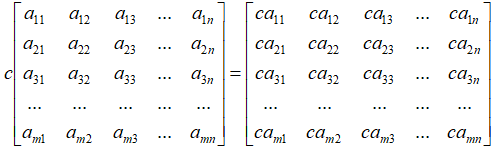
同样，我们来看一个实际例子的具体Python代码实现，求解矩阵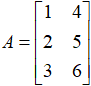
与数字2的乘法运算结果。
代码如下：
import numpy as np
A = np.array([[1, 4],
[2, 5],
[3, 6]])
print(2*A)
运行结果：
矩阵与矩阵之间的乘法运算，运算过程要稍微复杂一点。例如，我们下面举例的矩阵A和矩阵B的乘法运算，并不是说随意两个矩阵都可以进行相乘，乘法运算对两个矩阵的形态是有特定要求的。
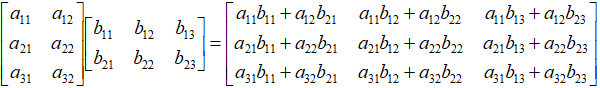
通过仔细观察上面的这个计算公式，我们可以总结出一些特殊要求和基本规律，主要有以下三条：
（1）左边矩阵的列数和右边矩阵的行数必须相等；
（2）左边矩阵的行数决定了最终结果矩阵的行数；
（3）右边矩阵的列数决定了最终结果矩阵的列数。
同样，我们用Python工具来实际演示一个乘法运算的例子，计算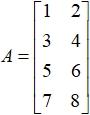矩阵
和矩阵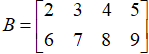
的乘法运算结果。
代码如下：
import numpy as np
A = np.array([[1, 2],
[3, 4],
[5, 6],
[7, 8]])
B = np.array([[2, 3, 4, 5],
[6, 7, 8, 9]])
print(np.dot(A, B))
运行结果：
[[ 14 17 20 23]
[ 30 37 44 51]
[ 46 57 68 79]
[ 62 77 92 107]]
矩阵与向量的乘法，一般而言是写成矩阵A在左，列向量x在右的Ax运算形式。这种Ax形式的写法便于描述向量x的空间位置在矩阵A的作用下进行变换的过程（下面会详细介绍这块内容）。
正如前面所讲的，矩阵与向量的乘法其实可以看作是矩阵与矩阵乘法的一种特殊形式，只不过位于后面的是一个列数为1的特殊矩阵而已。
具体的运算法则如下：
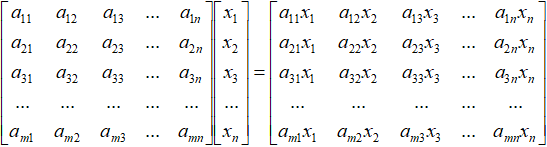
对照前面所讲过的矩阵与矩阵的乘法规则，我们来对比一下矩阵与向量的乘法规则，当我们把列向量看作是一个列数为1的特殊矩阵时，那么整个运算过程就会变得非常简单清晰：
（1）矩阵在左，列向量在右，矩阵的列数和列向量的维数必须相等；
（2）矩阵和列向量相乘的结果也是一个列向量；
（3）矩阵的行数就是结果向量的维数；
（4）乘法运算的实施过程就是矩阵的每行和列向量的对应元素分别相乘之后再进行相加。
我们来看一个矩阵与列向量相乘的例子：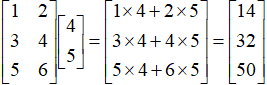
，并用Python语言来实际具体操作一下。
代码如下：
import numpy as np
A = np.array([[1, 2],
[3, 4],
[5, 6]])
x = np.array([[4, 5]]).T
print(np.dot(A, x))
运行结果：
从程序运行的结果来看，原始向量表示二维平面上的一个点，其平面坐标为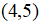
，经过矩阵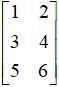
的乘法作用，最终将原始点转化成为了三维空间中的一个新的目标点，其空间坐标为
。
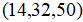因此，从这个例子中我们可以总结一下矩阵所发挥的重要作用：在指定矩阵的乘法作用下，原始空间中的向量被映射转换到了目标空间中的新坐标，向量的空间位置由此发生了变化，甚至在映射之后，目标空间的维数较之原始空间都有可能发生改变。那么，具体这些空间位置的改变有什么规律可言？在下一节里，我们会聚焦这一点，继续挖掘其背后更深层次的内涵。
本书所涉及的源代码已上传到百度网盘，供读者下载。请读者关注封底“博雅读书社”微信公众号，找到“资源下载”栏目，根据提示获取。
如果您对本书感兴趣，请进入当当网选购！
