|
|
创作新主题 |
| docker Elasticsearch |
| linux MongoDB Redis DATABASE NGINX 其他Web框架 web工具 zookeeper tornado NoSql Bootstrap js peewee Git bottle IE MQ Jquery |
| 机器学习算法 |
| 短视频 |
| 印度 |
在文章
【数据结构Python描述】树堆(heap)简介和Python手工实现及使用树堆实现优先级队列
中,为了能对优先级队列中键值对的增删都较为高效,我们基于
二叉堆
实现了
HeapPriorityQueue
。
对于使用
HeapPriorityQueue
创建的对象
q
,其中用于保存优先级队列键值对的二叉堆初始为空,如后续需要通过优先级队列操作的键值对数量为
n
n
n
,虽然我们大可以重复调用
n
n
n
次对象
q
的
add(k, v)
方法
来
构建堆
,但是根据文章
【常见算法Python描述】优先级队列应用之实现选择排序、插入排序和堆排序
的
分析
,该操作的最坏时间复杂度为
n
l
o
g
(
n
)
nlog(n)
n
l
o
g
(
n
)
。
如果 n n n 对键值对提前给定,如 【常见算法Python描述】优先级队列应用之实现选择排序、插入排序和堆排序 中具有 n n n 个元素的待排序集合,此时就可通过本文下面将介绍的 自底向上(Bottom-Up)方式构建二叉堆 ,这种方式的最坏时间复杂度为 O ( n ) O(n) O ( n ) 。
一、堆数据结构创建
为描述方便,下面介绍自底向上构建堆的方式时,假设给定数量为 n = 2 h + 1 − 1 n=2^{h+1}-1 n = 2 h + 1 − 1 (其中 h h h 为堆的高度 )的任意顺序键值对,则数量为 n n n 的键值对恰好可以填满高度为 h h h 的 完全二叉树 ,且每一层的键值对数量分别为 1 1 1 、 2 1 2^1 2 1 、 2 2 2^2 2 2 、 ⋅ ⋅ ⋅ \cdot\cdot\cdot ⋅ ⋅ ⋅ 、 2 h − 1 2^{h-1} 2 h − 1 、 2 h {2^h} 2 h ,此时二叉树的高度为 h = l o g ( n + 1 ) − 1 h=log(n+1)-1 h = l o g ( n + 1 ) − 1 。
1. 建堆步骤
下面以给定 n = 15 n=15 n = 1 5 个键值对为例介绍如何自底向上构建堆:
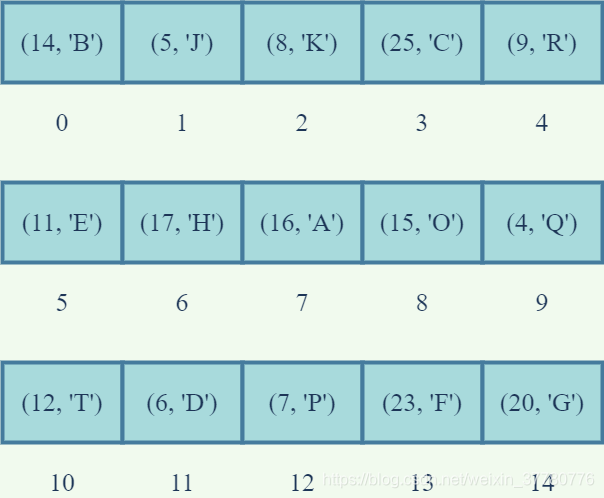
易知,上述 n = 15 n=15 n = 1 5 个键值对可以填满高度为 h = l o g ( 16 ) − 1 = 3 h=log(16)-1=3 h = l o g ( 1 6 ) − 1 = 3 的 完全二叉树 (但根据 堆的定义 ,此时 完全二叉树 还不是堆),如下图(a)所示:

下面的图(b)至图(h)介绍了具体的建堆过程:
- 第一步 (如图(b)所示),构建 ( 15 + 1 ) / 2 1 = 8 (15+1)/{2^1}=8 ( 1 5 + 1 ) / 2 1 = 8 个仅有一个键值对的堆:
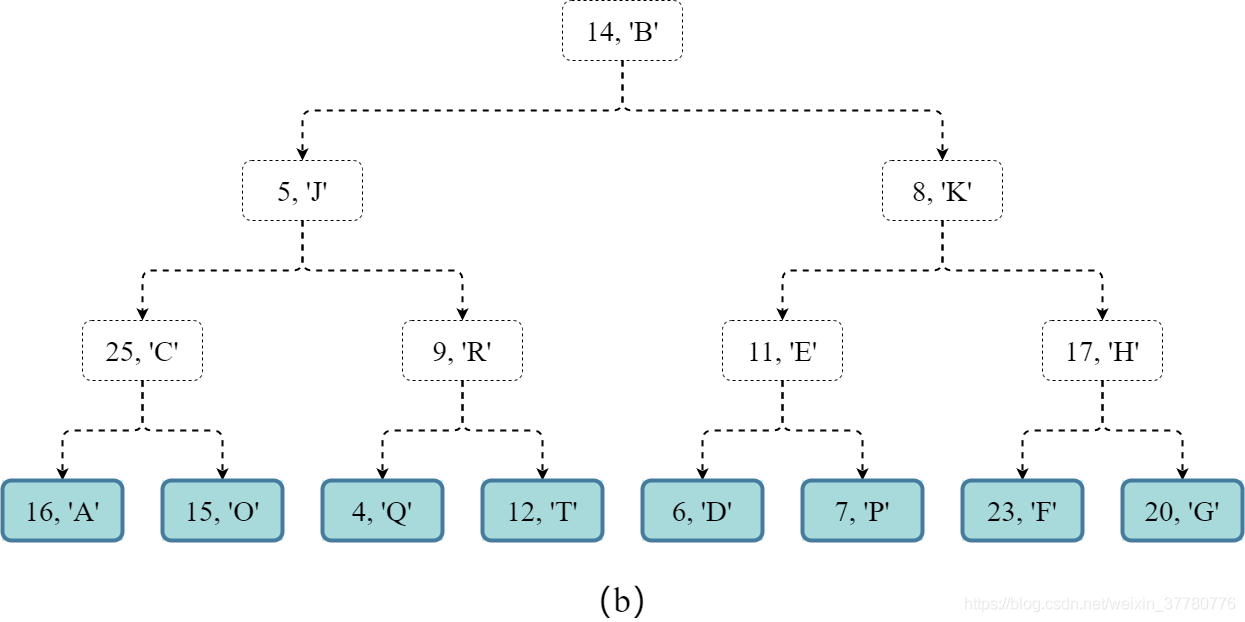
-
第二步
:
- 首先如图(c)所示,构建 ( 15 + 1 ) / 2 2 = 4 (15+1)/{2^2}=4 ( 1 5 + 1 ) / 2 2 = 4 个完全二叉树,每个包含 3 3 3 个键值对;
- 然后如图(d)所示,因为每个完全二叉树都可能违背 堆序性质 ,因此可能需要进行 父子结点间键值对的交换 ,最后才能得到 4 4 4 个 堆 。
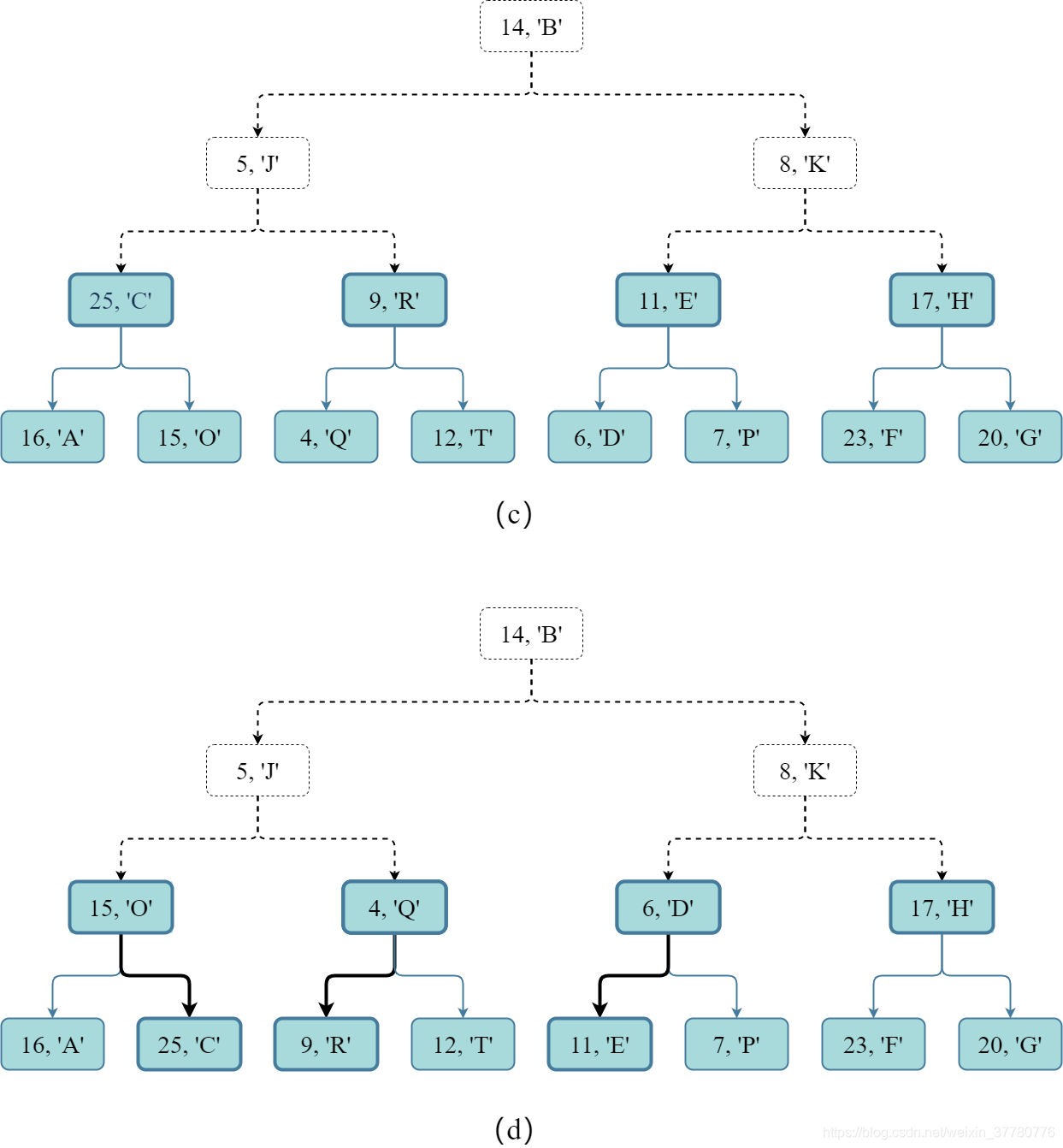
-
第三步
:
- 首先如图(e)所示,构建 ( 15 + 1 ) / 2 3 = 2 (15+1)/{2^3}=2 ( 1 5 + 1 ) / 2 3 = 2 个 完全二叉树 ,每个包含 7 7 7 个键值对;
- 然后如图(f)所示,因为每个 完全二叉树 都可能违背 堆序性质 ,因此可能需要进行 父子结点间键值对的交换 ,最后才能得到 2 2 2 个 堆 。
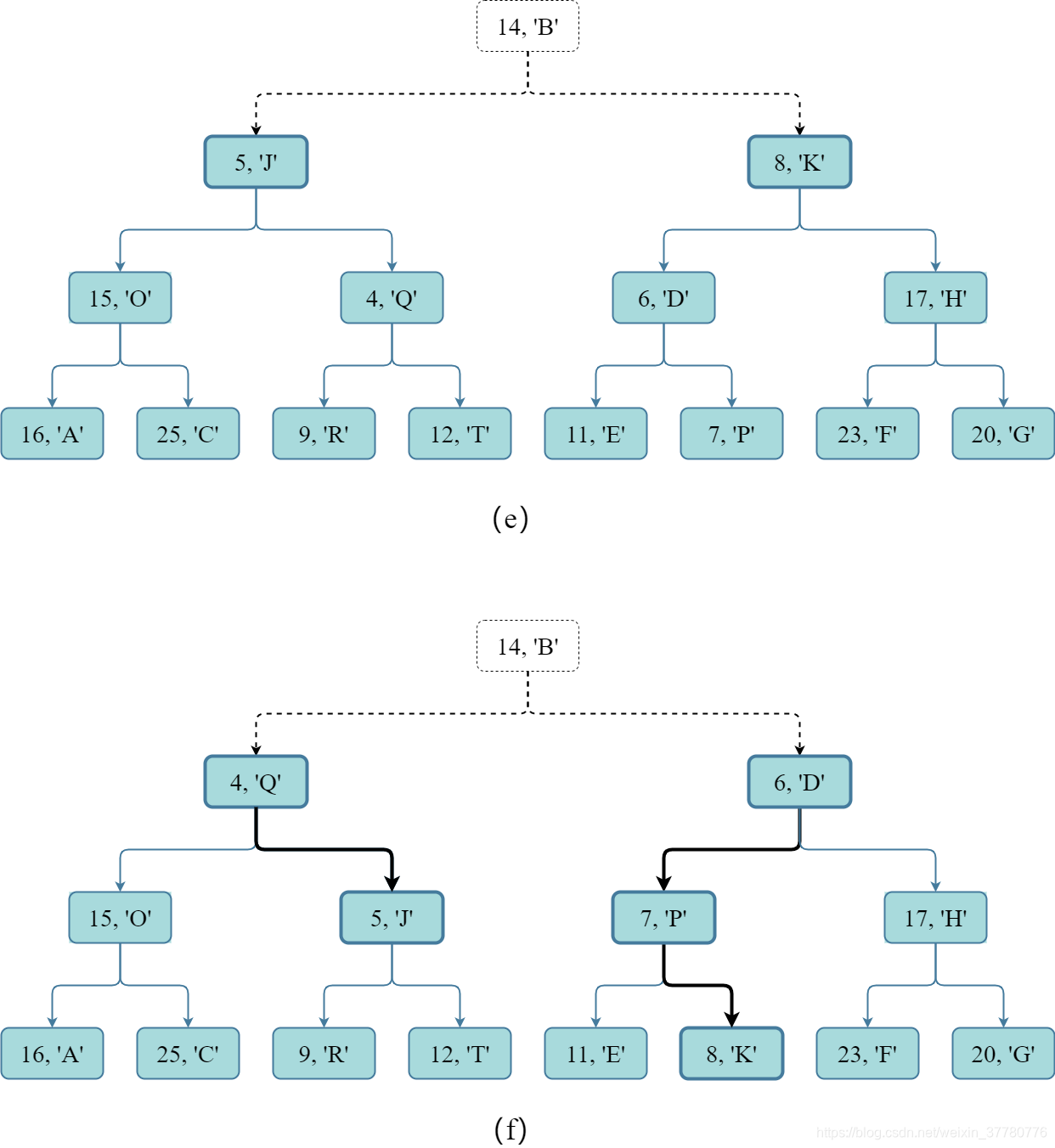
-
第四步
:
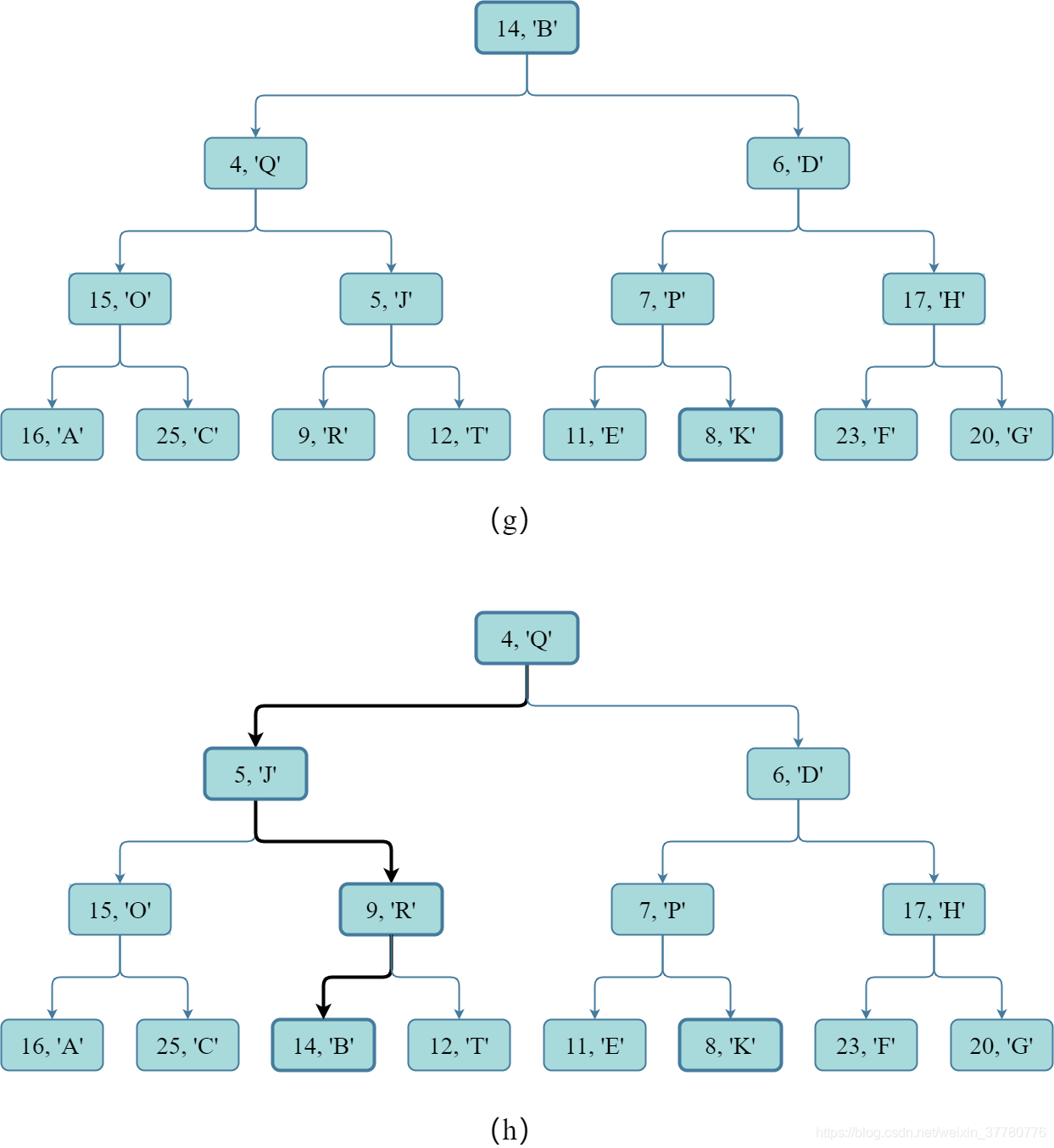
- 首先如图(g)所示,构建 ( 15 + 1 ) / 2 4 = 1 (15+1)/{2^4}=1 ( 1 5 + 1 ) / 2 4 = 1 个 完全二叉树 ,其中包含 15 15 1 5 个键值对;
- 然后如图(h)所示,因为该 完全二叉树 都可能违背 堆序性质 ,因此可能需要进行 父子结点间键值对的交换 ,最后才能得到根据给定的 15 15 1 5 个键值对需构建的 1 1 1 个 二叉堆 。
2. 建堆实现
分析上述建堆过程可知,实现建堆最重要的是如何将两个形态和大小完全相同的 子堆 在根结点处进行合并,且保证合并后得到的 完全二叉树 是一个 二叉堆 。
实际上,对于以列表方式给出键值对形式结点元素的
完全二叉树
,文章
【数据结构Python描述】树堆(heap)简介和Python手工实现及使用树堆实现优先级队列
中介绍的
自堆顶向下冒泡
算法实现
_downheap()
恰好可以满足该需求。
具体地,在实现上述建堆过程时,只需要对
完全二叉树
从最底层最右侧结点开始直到根结点的每一个结点使用一个循环,依次调用
_downheap()
方法
即可。
更进一步地,因为
_downheap()
方法
不对
叶子结点
执行任何操作,所以上述循环只需从最底层的非叶子结点开始依次调用
_downheap()
方法
。
对上述分析使用Python实现如下:
def __init__(self, contents=tuple()):
"""
初始化一个优先级队列
默认将新创建的优先级队列初始化为空,如果提前给定元素为(k, v)形式的contents集合,则使用contents初始化优先级队列
:param contents:(k, v)形式元素contents集合
"""
self._data = [self._Item(k, v) for k, v in contents]
if len(self._data) > 1
:
self._heapify()
def _heapify(self):
"""
具体执行自底向上建堆
:return: None
"""
start = self._parent(len(self) - 1) # 从最后一个叶子结点的父结点开始
for j in range(start, -1, -1): # 自底向上
self._downheap(j)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
分析上述代码可知,建堆实现只是将
HeapPriorityQueue
的
__init__()
方法
进行了重新设计并提供了一个非公有的实用方法
_heapify()
,其逻辑为:在使用
HeapPriorityQueue
创建对象时,其初始化方法接收一个可选参数
contents
,该参数是元素为
(k, v)
形式的元组,与旧的初始化方法不同的是,这里使用列表推导式初始化后续建堆用的列表。
3. 建堆效率
为了分析自底向上建堆的实现
_heapify()
方法的时间复杂度,这里:
- 首先给出结论:
针对提前给定的 n n n 个键值对,如采用自底向上的方式构建堆,则假定键值对间两两比较的时间复杂度为 O ( 1 ) O(1) O ( 1 ) ,则该建堆方式的最坏时间复杂度为 O ( n ) O(n) O ( n ) 。
- 然后以上述给定的 15 15 1 5 个键值对为例进行验证;
- 最后再进行一般性分析。
对于给定具有任意顺序的 15 15 1 5 个键值对 :
在
_heapify()
中,最坏情况下,循环每一次迭代的运行时间正比于当前结点到最底层结点(此处为第
4
4
4
层结点)的
高度
,因此:
-
第
4
4
4
层结点数量为
2
3
=
8
2^{3}=8
2
3
=
8
,但是
_heapify()不对这些结点执行任何操作,因此本层的时间复杂度为 0 0 0 ; -
第
3
3
3
层结点数量为
2
2
=
4
2^{2}=4
2
2
=
4
,当前所有结点到最底层结点(此处为第
4
4
4
层结点)的
高度
为
1
1
1
,则对该层每个结点调用
_downheap()的最坏时间复杂度正比于 4 × 1 = 4 4\times1=4 4 × 1 = 4 ; -
第
2
2
2
层结点数量为
2
1
=
2
2^{1}=2
2
1
=
2
,当前所有结点到最底层结点(此处为第
4
4
4
层结点)的
高度
为
2
2
2
,则对该层每个结点调用
_downheap()的最坏时间复杂度正比于 2 × 2 = 4 2\times2=4 2 × 2 = 4 ; -
第
1
1
1
层结点数量为
2
0
=
1
2^{0}=1
2
0
=
1
,当前所有结点到最底层结点(此处为第
4
4
4
层结点)的
高度
为
3
3
3
,则对该层每个结点调用
_downheap()的最坏时间复杂度正比于 1 × 3 = 3 1\times3=3 1 × 3 = 3 。
综上,即
_heapify()
的最坏时间复杂度正比于
4
+
4
+
3
=
11
<
15
4+4+3=11<15
4
+
4
+
3
=
1
1
<
1
5
。
一般地, 对于给定具有任意顺序的 n = 2 h + 1 − 1 n=2^{h+1}-1 n = 2 h + 1 − 1 个键值对 :
-
第
h
h
h
层结点数量为
2
h
2^h
2
h
,但是
_heapify()不对这些结点执行任何操作,因此本层的时间复杂度为 0 0 0 ; -
第
h
−
1
h-1
h
−
1
层结点数量为
2
h
−
1
2^{h-1}
2
h
−
1
,当前所有结点到的
高度
为
1
1
1
,则对该层每个结点调用
_downheap()的最坏时间复杂度正比于 2 h − 1 × 1 {2^{h-1}}\times1 2 h − 1 × 1 ; -
第
h
−
2
h-2
h
−
2
层结点数量为
2
h
−
2
2^{h-2}
2
h
−
2
,当前所有结点到的
高度
为
2
2
2
,则对该层每个结点调用
_downheap()的最坏时间复杂度正比于 2 h − 2 × 2 {2^{h-2}}\times2 2 h − 2 × 2 ; - ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ \cdot\cdot\cdot\cdot\cdot\cdot ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
-
第
h
−
j
h-j
h
−
j
层结点数量为
2
h
−
j
2^{h-j}
2
h
−
j
,当前所有结点到的
高度
为
j
j
j
,则对该层每个结点调用
_downheap()的最坏时间复杂度正比于 2 h − j × j {2^{h-j}}\times{j} 2 h − j × j ; - ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ \cdot\cdot\cdot\cdot\cdot\cdot ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
-
第
0
0
0
层结点数量为
2
0
2^{0}
2
0
,当前所有结点到的
高度
为
h
h
h
,则对该层每个结点调用
_downheap()的最坏时间复杂度正比于 2 0 × h {2^{0}}\times{h} 2 0 × h 。
因此,总的建堆时间复杂度正比于:
f ( n ) = ∑ j = 0 h j 2 h − j f(n)=\sum\nolimits_{j=0}^{h}{j}{2^{h-j}} f ( n ) = ∑ j = 0 h j 2 h − j
变形后得:
f ( n ) = 2 h ∑ j = 0 h j 2 j f(n)={2^h}\sum\nolimits_{j=0}^{h}{\frac{j}{2^j}} f ( n ) = 2 h ∑ j = 0 h 2 j j
因此,重点是求下列表达式的和:
∑ j = 0 h j 2 j \sum\nolimits_{j=0}^{h}{\frac{j}{2^j}} ∑ j = 0 h 2 j j
为了求出上述表达式的和,需要使用下面的数学技巧:
- 首先,根据高中数学知识,对任意 x < 1 x\lt1 x < 1 ,有下列等比数列求和公式:
∑ j = 0 ∞ x j = 1 1 − x \sum\nolimits_{j=0}^{\infty}{x^j}=\frac{1}{1-x} ∑ j = 0 ∞ x j = 1 − x 1
- 然后,上述等式两端对 x x x 求导后得:
∑ j = 0 ∞ j x j − 1 = 1 ( 1 − x ) 2 \sum\nolimits_{j=0}^{\infty}{j}{x^{j-1}}=\frac{1}{(1-x)^2} ∑ j = 0 ∞ j x j − 1 = ( 1 − x ) 2 1
上式两边同乘以 x x x 后得:
∑ j = 0 ∞ j x j = x ( 1 − x ) 2 \sum\nolimits_{j=0}^{\infty}{j}{x^{j}}=\frac{x}{(1-x)^2} ∑ j = 0 ∞ j x j = ( 1 − x ) 2 x
- 最后,如果令上述等式 x = 1 / 2 x={\left.1\middle/2\right.} x = 1 / 2 ,则:
∑ j = 0 ∞ j 2 j = 1 / 2 ( 1 − ( 1 / 2 ) ) 2 = 2 \sum\nolimits_{j=0}^{\infty}\frac{j}{2^j}=\frac{ {\left.1\middle/2\right.}}{(1-({\left.1\middle/2\right.}))^2}=2 ∑ j = 0 ∞ 2 j j = ( 1 − ( 1 / 2 ) ) 2 1 / 2 = 2
因此:
f ( n ) = 2 h ∑ j = 0 h j 2 j < 2 h ∑ j = 0 ∞ j 2 j = 2 h × 2 = 2 h + 1 f(n)={2^h}\sum\nolimits_{j=0}^{h}{\frac{j}{2^j}}\lt{ {2^h}\sum\nolimits_{j=0}^{\infty}{\frac{j}{2^j}}}=2^h\times{2}=2^{h+1} f ( n ) = 2 h ∑ j = 0 h 2 j j < 2 h ∑ j = 0 ∞ 2 j j = 2 h × 2 = 2 h + 1
又本节开头假定 n = 2 h + 1 − 1 n=2^{h+1}-1 n = 2 h + 1 − 1 ,于是 f ( n ) < n + 1 ∈ O ( n ) f(n)\lt{n+1}\in{O(n)} f ( n ) < n + 1 ∈ O ( n ) 。至此,证毕。
二、完整测试代码
下面是针对
【数据结构Python描述】树堆(heap)简介和Python手工实现及使用树堆实现优先级队列
中实现的
HeapPriorityQueue
,使用自底向上建堆方法完善后得到的最终结果及其测试代码:
# heap_priority_queue.py
from priority_queue import PriorityQueueBase
class Empty(Exception):
"""尝试对空优先级队列进行删除操作时抛出的异常"""
pass
class HeapPriorityQueue(PriorityQueueBase):
"""使用堆存储键值对形式记录的优先级队列"""
def __init__(self, contents=tuple()):
"""
初始化一个优先级队列
默认将新创建的优先级队列初始化为空,如果提前给定元素为(k, v)形式的contents集合,则使用contents初始化优先级队列
:param contents:(k, v)形式元素contents集合
"""
self._data = [self._Item(k, v) for k, v in contents]
if len(self._data) > 1:
self._heapify()
def _heapify(self):
"""
具体执行自底向上建堆
:return: None
"""
start = self._parent(len(self) - 1) # 从最后一个叶子结点的父结点开始
for j in range(start, -1, -1): # 自底向上
self._downheap(j)
def _parent(self, j):
"""
返回父结点处业务元素在列表中的索引
:param j: 任意结点处的业务元素在列表中的索引
:return: 父结点处业务元素在列表中的索引
"""
return (j - 1) // 2
def _left(self, j):
"""
返回左子结点处业务元素在列表中的索引
:param j: 任意结点处的业务元素在列表中的索引
:return: 左子结点处业务元素在列表中的索引
"""
return 2 * j + 1
def _right(self, j):
"""
返回右子结点处业务元素在列表中的索引
:param j: 任意结点处的业务元素在列表中的索引
:return: 右子结点处业务元素在列表中的索引
"""
return 2 * j + 2
def _has_left(self, j):
"""
如结点有左子结点则返回True,否则返回False
:param j: 任意结点处的业务元素在列表中的索引
:return: 判断结点是否有左子结点的Boolean结果
"""
return self._left(j) < len(self._data) # 确保列表索引不越界
def _has_right(self, j):
"""
如结点有右子结点则返回True,否则返回False
:param j: 任意结点处的业务元素在列表中的索引
:return: 判断结点是否有右子结点的Boolean结果
"""
return self._right(j) < len(self._data) # 确保列表索引不越界
def _swap(self, i, j):
"""
交换一对父子结点的业务元素
:param i: 业务元素在列表中的索引
:param j: 业务元素在列表中的索引
:return: None
"""
self._data[i], self._data[j] = self._data[j], self._data[i]
def _upheap(self, j):
"""
自堆底向上冒泡算法
:param j: 结点处业务元素在列表中的索引
:return: None
"""
parent = self._parent(j)
if j > 0 and self._data[j] < self._data[parent]:
self._swap(j, parent)
self._upheap(parent) # 递归调用
def _downheap(self, j):
"""
自堆顶向下冒泡算法
:param j: 结点处业务元素在列表中的索引
:return: None
"""
if self._has_left(j):
left = self._left(j)
small_child = left
# 如果有左、右两个子结点,令small_child引用键较小子结点的业务元素在列表中的索引
if self._has_right(j):
right = self._right(j)
if self._data[right] < self._data[left]:
small_child = right
# 至少根结点有左子结点时,才有可能self虽然是完全二叉树但不是堆
if self._data[small_child] < self._data[j]:
self._swap(j, small_child)
self._downheap(small_child) # 递归调用
def __len__(self):
"""返回优先级队列中的记录条目数"""
return len(self._data)
def __iter__(self):
"""生成优先级队列中所有记录的一个迭代"""
for each in self._data:
yield each
def add(self, key, value):
"""向优先级队列中插入一条key-value记录"""
self._data.append(self._Item(key, value)) # 新记录条目插入并确保完全二叉树性质
self._upheap(len(self._data) - 1) # 确保满足堆序性质
def min(self):
"""返回(但不删除)优先级队列中键最小的记录,如优先级队列此时为空则抛出异常"""
if self.is_empty():
raise Empty('优先级队列为空!')
item = self._data[0]
return item.key, item.value
def remove_min(self):
"""回并删除优先级队列中键最小的记录,如优先级队列此时为空则抛出异常"""
if self.is_empty():
raise Empty('优先级队列为空!')
self._swap(0, len(self._data) - 1) # 将根结点处键最小记录交换至完全二叉树最底层最右侧结点处
item = self._data.pop()
self._downheap(0) # 确保完全二叉树满足堆序性质,即确定需保存在根结点处的键最小记录
return item.key, item.value
if __name__ == '__main__':
heap_queue = HeapPriorityQueue()
print(heap_queue.is_empty()) # True
heap_queue.add(4, 'C')
heap_queue.add(6, 'Z')
heap_queue.add(7, 'Q')
heap_queue.add(5, 'A')
print(heap_queue) # [(4, 'C'), (5, 'A'), (7, 'Q'), (6, 'Z')]
heap_queue.add(2, 'T')
print(heap_queue) # [(2, 'T'), (4, 'C'), (7, 'Q'), (6, 'Z'), (5, 'A')]
print(heap_queue.remove_min()) # (2, 'T')
print(heap_queue.remove_min()) # (4, 'C')
print(heap_queue) # [(5, 'A'), (6, 'Z'), (7, 'Q')]
print(heap_queue.min()) # (5, 'A')
print(heap_queue.is_empty()) # False
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
实际上,虽然我们在分析
自底向上建堆
方式时假设给定的价值对个数为
n
=
2
h
+
1
−
1
n=2^{h+1}-1
n
=
2
h
+
1
−
1
个,但实际上对于任意数量的键值对,上述实现的
_heapify()
方法均支持,具体留待读者思考。
三、参考资料
本文地址:http://www.python88.com/topic/74115









