由线性回归来理解深度学习的理论基础

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

这会是一篇比较长的文章，本来应该是分几次来po，但考虑到这个话题的整体性，因此这里还是整理到一篇文章里，感兴趣的同学可以点个收藏慢慢看。

以下为作者原文：

在这篇文章中，我将试着从机器学习的简单算法开始解释深度学习。这种理解深度学习的方法将在我的新书当中详细介绍，您可以在Linkedin上与我（Ajit Jaokar）联系以了解有关该书的更多信息。我在教学中使用过这种方法，我把它称之为“例外学习，即理解一个概念及其局限性，然后理解后续概念以及如何克服该局限性。

这篇文章将会由以下内容依次构成：

• 线性回归（Linear Regression）

• 多元线性回归（Multiple Linear Regression）

• 多项式回归（Polynomial Regression）

• 广义线性模型（Generalised Linear Model）

• 感知器学习（Perceptron Learning）

• 多层感知器（Multi-Layer Perceptron Learning）

  
  

由此我们形成了一个链式思想：从线性回归开始，而后扩展到多层感知器（深度学习）。另外，为简单起见，我们这里不去讨论其他形式的深度学习，例如CNN和LSTM，在这篇文章种我们所讨论的深度学习仅限于多层感知器。

为什么从线性回归开始？因为即使在高中阶段，我们也开始接触到了这个概念。首先从“学习”这个概念讲起，在机器学习（监督学习）中，学习的过程即寻找一个数学方程式，从而使得每一个输入和输出都能够通过这个方程一一对应。

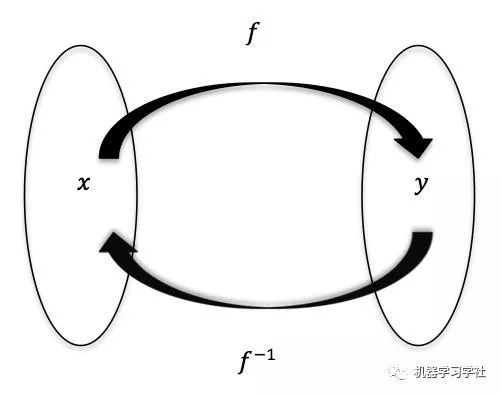
在最简单的情境下，这个方程是线性的。

什么是线性关系？

线性关系指的是可以用一条直线表示的两个变量（x和y）之间的关系。许多现象都是线性关系，如双手拉橡皮所使用的力量和橡皮被拉伸的长度，我们可以用线性方程来表示如上关系：

在线性关系中，改变自变量（x）的值会导致因变量（y）的值发生改变，因此线性关系可以用来预测诸如销售预估、用户行为分析等实际问题。

线性关系如下图所示：

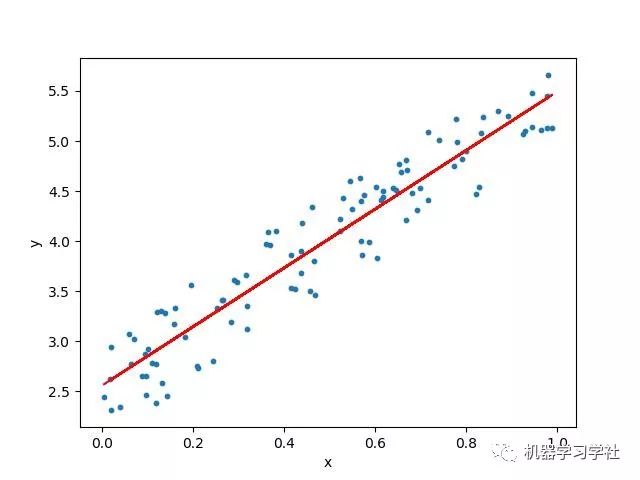
线性回归问题意在寻找可以描述一个或多个特征（自变量）与目标值（因变量）之间关系的方程。如上图所示的线性回归问题，我们通常称之为普通线性回归，即最简单的线性回归。

现在我们来考虑由简单线性回归引申出的三个问题：

1. 多元线性回归

2. 广义线性模型

3. 多项式回归

普通线性回归的第一个明显变体是多元线性回归。当只有一个特征时，我们有单变量线性回归，如果有多个特征，我们有多元线性回归。对于多元线性回归，模型可以以一般形式表示为：

模型的训练即寻找最佳参数θ，以使模型最贴合数据。预测值与目标值之间的误差最小的直线称为最佳拟合线或回归线，这些误差被称为残差（Residuals）。可以通过从目标值到回归线的垂直线来可视化残差，如下图所示，灰色直线即回归线，紫色点为目标值，黄色垂直距离即残差。

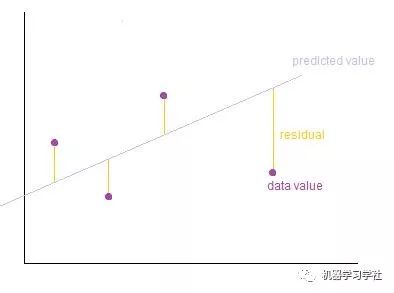
我们将整个模型的误差（即损失函数）定义为残差平方和，表示如下：

最经典的多元线性回归问题是波士顿房价问题（Boston Housing Dataset）

在普通线性回归中，预测变量（x）的变化会导致响应变量（y）的变化，但是，当且仅当响应变量具有正态分布时才成立。在响应变量是正态分布时，有好多问题我们无法处理：1）响应变量总是为正且在很大范围内变化；2）预测变量的变化导致响应变量的几何变换，而不是连续变化（即两者间非线性关系）。

广义线性回归是由普通线性回归延伸出的第二个模型，它满足：1）响应变量可以不是正态分布；2）允许响应变量不是随着预测变量线性变化。

介绍了多元回归和GLM之后，让我们现在看一下我们可以从普通线性回归推断出的第三个模型——多项式回归。在多项式回归中，自变量x和因变量y之间的关系被表示为x的n次多项式的形式。多项式回归已被用于描述非线性现象，如组织的生长速度，湖泊沉积物中碳同位素的分布，以及疾病流行的进展。

接下来我们看看感知器是如何与线性回归模型产生联系的。        

感知器（Perceptrons）是用于二元分类问题的监督学习算法，二元分类器是二类问题的线性分类器。Mark I 感知器是感知器算法的第一个实现，感知器算法由Frank Rosenblatt于1957年在康奈尔航空实验室发明，感知器旨在成为一台机器，而不是一个程序，这台机器专为图像识别而设计：它有一个由400个光电池组成的阵列，随机连接到“神经元”，权重由电位器编码，并且在学习期间通过机器执行权重更新。在美国海军组织的1958年新闻发布会上，Rosenblatt发表了关于感知者的声明，这一声明引起了人工智能社区的激烈争论。根据罗森布拉特的声明，感知器是“电子计算机的胚胎，走路，说话，看，写，复制自己，并感受到它的存在。”

单层感知器仅能够学习线性可分离的模式。1969年，一本名为Perceptrons的书表明，感知器网络不可能学习XOR功能。但是，如果我们使用非线性激活函数（而不是梯度函数），则可突破此限制。事实上，通过使用非线性激活函数，我们可以构建比XOR更复杂的函数（即使只有单层），如果我们添加更多隐藏层，则可以拓展处更复杂的功能，即我们接下来要介绍的多层感知器（深度学习）。

我们回顾一下：

1）感知器是生物神经元的简化模型。

2）感知器是用于学习二元分类器的算法：将其输入映射到输出值的函数。

3）在神经网络的背景下，感知器是使用Heaviside阶跃函数作为激活函数的人工神经元，感知器算法也称为单层感知器，以区别于多层感知器。

4）Perceptron算法具有历史意义，但它为我们提供了一种拉近线性回归和深度学习之间差别的方法。

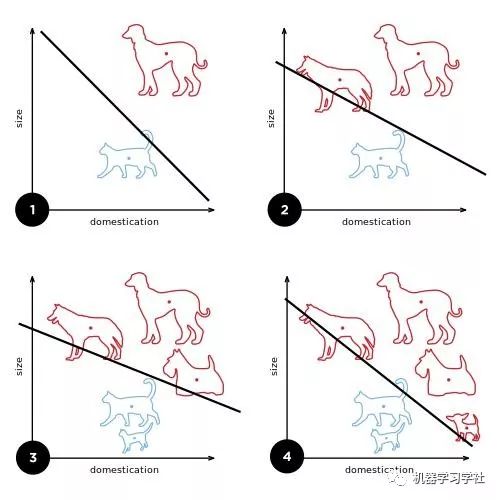
5）单层感知器的学习过程如下所示，每加入一个数据点，感知器便会更新一次线性边界，类似于线性回归中的回归线。

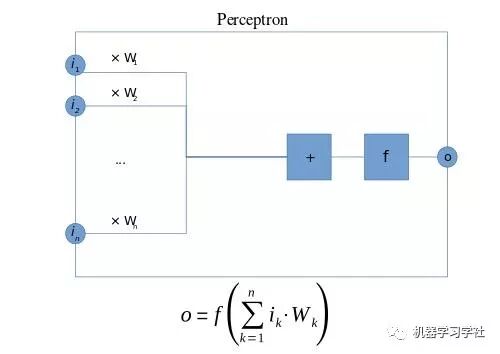
下图为感知器的示意图，f为阶跃函数，输出为二进制（0或1），i1-in为输入，Wi为各个输入的权重：

现在我们来介绍多层感知器（MLP）。通过添加非线性的激活函数以及使用多层网络的结构，多层感知器延展了单层感知器的功能。在训练中，我们需要用到反向传播和梯度下降的方式来更新权重。多层感知器的构造如图所示：

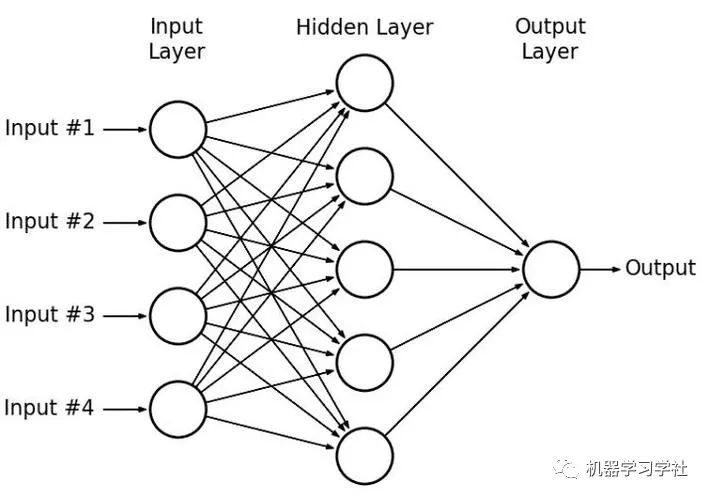
多层感知器的“多层”结构可以从数据当中提取层次性的结构（每一层都可以从上一层当中提取一次特征），从而找到更好地模拟数据规律的方式。

因此，具有单层无激活功能（或阶跃激活功能）的神经网络（即多层感知器）等同于线性回归。此外，线性回归可以使用封闭形式解决方案来解决。然而，随着MLP的结构更加复杂，封闭形式的解决方案不再管用，因此必须使用迭代解决方案，即通过逐步改进的方法来改善结果。这样的算法不一定会收敛，梯度下降就是一个经典的例子。

MLP（深度学习）是一个高度参数化的模型。对于等式y = mx + c，m和c被称为参数，我们从数据和中推导出参数的值。方程的参数可以看作自由度，线性回归具有相对较少的参数，即具有较小的自由度。然而，更复杂的MLP具有更多的参数，也具有更大的自由度。虽然两者都是参数化模型，但MLP的优化策略（反向传播+梯度下降）比线性回归的优化策略（最小二乘法）复杂得多。从这个方面讲，神经网络可以看作是线性回归的复杂衍生物，多层感知器的高度参数化允许我们构建功能更加复杂的模型。

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~