作者 | Andrea Cognolato 译者 | 弯月
出品 | CSDN（ID：CSDNnews）
简介
在这篇文章中，我将介绍概率编程语言（Probabilistic Programming Languages，简称PPL）的工作原理，并逐步演示如何用Python构建一个简单的概率编程语言。
本文主要面向的读者是统计学家、AI研究员和好奇的程序员，相信大家都熟悉 PPL 和贝叶斯统计，并掌握了基本的 Python知识。
我们将要构建的API如下：
mu =LatentVariable("mu",Normal, [0.0, 5.0])y_bar =ObservedVariable("y_bar", Normal, [mu, 1.0],observed=3.0)
evaluate_log_density(y_bar,{"mu": 4.0})
前两行定义了统计模型：
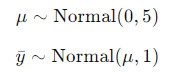
最后一行求在
条件下，在 μ = 4 处该模型定义的（未正规化的）概率分布。
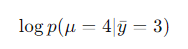
希望本文能让读者理解 PPL 的工作原理，并了解如何用 Python 实现一门嵌入式领域专用语言（Embedded Domain-Specific Languages，简称EDSL）。
相关研究
据我所知，目前尚没有使用Python的PPL实现。
《TheDesign and Implementation of Probabilistic Programming Languages》一书的重点是编程语言理论，需要读者熟悉 continuation-passing style、协程，而且采用了JavaScript 作为实现语言。
《Anatomyof a Probabilistic Programming Framework》一文（https://www.georgeho.org/prob-prog-frameworks/）是很不错的高层概要，但并没有涉及具体实现细节和代码示例。
Junpeng Lao的演讲（https://www.youtube.com/watch?v=WHoS1ETYFrw&feature=youtu.be）和 PyMC3的开发者指南（https://docs.pymc.io/en/v3/developer_guide.html）描述了 PyMC 的具体实现细节，但想根据这些内容实现一个 PPL 并不容易。
实现
高层表示
我们使用下述模型作为基本的参考：
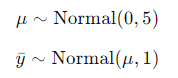
这两个表达式定义了一个联合概率分布，对应的概率密度函数（Probability Density Function，简称PDF）为：
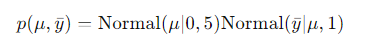
可以用两种形式的图来表示这个表达式（和模型）：一种是图模型，一种是有向因子图。
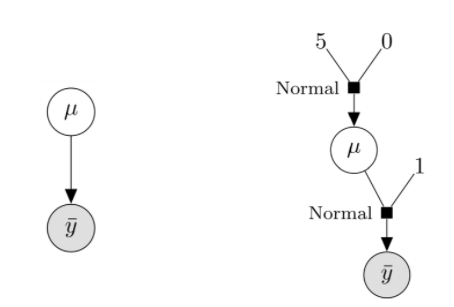
左：用概率图模型（PGM）表示的模型。右：用有向因子图表示的模型。
虽然在各类文档中PGM方式更常见，但我认为LFG对于实现PPL的人来说更有用。这个图揭示了几个重要方面：
一种是观测到的值（，灰色背景）
一种是无法观测到的隐变量（μ，白色背景）
在文本中，分布指的是一个类，它带有一个函数，可以求在某个点上的对数概率密度。log_density 函数接受一个 float 类型的参数，表示分布支持的一个点；一个 List[float]，表示分布的参数；返回一个 float，是该分布在该点上的对数PDF。要实现新的分布，只需从 Distribution 虚类集成即可。暂时不支持向量或矩阵分布。
我们使用 SciPy 实现一个 Normal 分布，param[0] 是均值，param[1] 是标准差。
from scipy.stats import norm
classDistribution: @staticmethod def log_density(point, params): raise NotImplementedError("Mustbe implemented by a subclass")
classNormal(Distribution): @staticmethod def log_density(point, params): returnfloat(norm.logpdf(point, params[0], params[1]))
变量和DAG
现在我们来看看变量。这些变量包含三个方面：它们有关联的分布，可以为隐变量或观测变量，它们之间互相连接（即变量可以有子变量）。
dist_class字段就是变量关联的分布 Distribution。在需要求完整的对数密度时，我们会使用该字段访问变量的分布的log_density方法。
区分隐变量和观测变量的方式是使用 LatentVariable 和 ObservedVariable 类。观测变量有一个observed 字段，其中包含了观测的值。由于隐变量在建模阶段没有值，我们必须在运行时给其复制，才能求出全部的对数分布。要在运行时给隐变量复制，我们需要用唯一的字符串 name 来区分它们。
最后，我们可以将一个变量的分布的参数设置为变量或常量。在本例中，的平均值是 μ，一个正太随机变量，而它的标准差是常数 1。为了表示它，我们使用 dist_args 属性。mypy 中的 dist_args 的签名为 dist_args: Union[float, LatentVariable, ObservedVariable]。这就是说，一个隐变量或观测变量可以有“参数”，参数本身也可以是常量的隐变量或观测变量，这就创建了一个有向无环图（DAG）。
classLatentVariable: def __init__(self, name, dist_class, dist_args): self.name = name self.dist_class = dist_class self.dist_args = dist_args
classObservedVariable: def __init__(self, name, dist_class, dist_args, observed): self.name = name self.dist_class = dist_class self.dist_args = dist_args self.observed = observed
可视化该DAG，就会注意到它和隐因子图之间的一个重要区别：箭头方向是相反的。其原因是我们的建模API中的变量指定方式。而且，似乎将观测变量作为根节点，能更好地表示计算联合对数密度的过程。
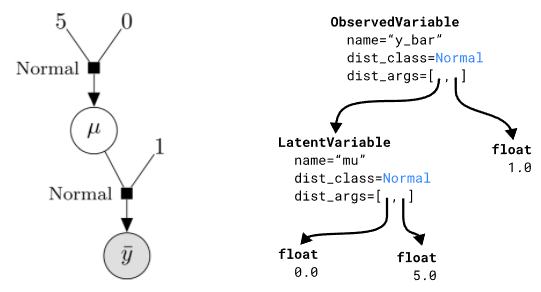
左：将模型表示为有向因子图。右：内存中的DAG表示。
为了进一步说明，我们来看看模型中的 dist_args 是什么样子：
mu =LatentVariable("mu",Normal, [0.0, 5.0])y_bar =ObservedVariable("y_bar", Normal, [mu, 1.0],observed=5.0)
print(mu)#=> <__main__.latentvariable object at>print(mu.dist_args)#=> [0.0, 5.0]print(y_bar)#=> <__main__.observedvariable object at>print(y_bar.dist_args)# => [<__main__.latentvariable object at>,1.0]
求出对数密度
我们距离目标不远了，现在还缺一种通过DAG计算联合对数密度的方法。我们需要遍历DAG，将每个变量的对数密度加在一起。对数密度加法相当于密度的乘法，但加法在数值上更稳定。
遍历DAG需要使用一个递归算法，叫做深度优先搜索。collect_variables函数会访问所有变量一次，将所有非float变量收集到一个列表中。然后算法从根节点开始，递归地遍历收集到的每个变量的所有dist_args。
defevaluate_log_density(variable, latent_values): visited = set() variables = []
def collect_variables(variable): if isinstance(variable, float): return
visited.add(variable) variables.append(variable)
for arg in variable.dist_args: if arg not in visited: collect_variables(arg)
collect_variables(variable)
对于每个变量，我们需要获取它的每个参数的数值，然后用它求出分布的对数密度。由于float参数已经是数值了，而LatentVariables根据求值所在的位置不同而有不同的值。为了指定隐变量的值，我们需要传递一个包含了从变量名到数值的映射的字典，名为latent_values。注意ObservedVariables不能是参数，只能是根节点。
注意：
最后，我们有了从参数中提取出的分布参数，就可以更新整体的对数密度了。LatentVariable需要在latent_values指定的点上计算对数密度，而ObservedValues会在observed指定的点上计算对数密度。
log_density = 0.0 for variable in variables: dist_params = [] for dist_arg in variable.dist_args: if isinstance(dist_arg, float): dist_params.append(dist_arg) if isinstance(dist_arg, LatentVariable): dist_params.append(latent_values[dist_arg.name])
if isinstance(variable, LatentVariable): log_density +=variable.dist_class.log_density(
latent_values[variable.name],dist_params ) if isinstance(variable, ObservedVariable): log_density +=variable.dist_class.log_density( variable.observed, dist_params )
returnlog_density
我们来检查一下整体的对数概率是否与期待的结果一致：
mu =LatentVariable("mu",Normal, [0.0, 5.0])y_bar =ObservedVariable("y_bar", Normal, [mu, 1.0],observed=5.0)
latent_values = {"mu": 4.0}print(evaluate_log_density(y_bar, latent_values))#=> -4.267314978843446print(norm.logpdf(latent_values["mu"], 0.0, 5.0) + norm.logpdf(5.0, latent_values["mu"], 1.0))# => -4.267314978843446
结论和改进
分布、变量DAG和对数密度计算是概率编程语言的组成部分。变量可以是隐变量或观测变量，在计算对数密度时，每个变量必须单独处理。我们用Python实现了这些概念，从而实现了简单但强大的PPL。
下一步是增加对张量和随机变量变换的支持，从而支持更有用的模型，如线性回归、层次/混合效果模型等。另一个有用的特性是构建一个API用于先验预测采样。最后，我们可以不在Python中进行计算，而是使用像Theano/Aesara、Jax或TensorFlow之类的计算图框架，可以极大地改善性能。计算图还可以通过反式自动微分的方式，利用对数密度计算梯度，这可以用于汉密尔顿·蒙特卡洛等更高级的采样器上。
篇外：后验网格近似
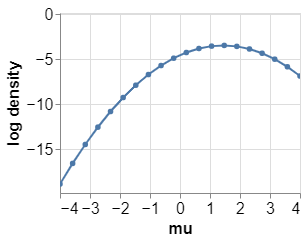
下面，我们讨论一下对数密度的用途。其用途之一就是找到后验分布的模，即找到参数的最有可能的值。
本例中，观测样本的平均值是1.5，在正态零均值先验的条件下，它会向 0 移动一点。这就是说，最大后验估计（Maximum A Posteriori estimate）大约是1.4。
import numpy as npimport pandas as pdimport altair as altfrom smolppl import Normal, LatentVariable, ObservedVariable, evaluate_log_density
参考链接：
https://mrandri19.github.io/2022/01/12/a-PPL-in-70-lines-of-python.html
《新程序员003》正式上市，50余位技术专家共同创作，云原生和数字化的开发者们的一本技术精选图书。内容既有发展趋势及方法论结构，华为、阿里、字节跳动、网易、快手、微软、亚马逊、英特尔、西门子、施耐德等30多家知名公司云原生和数字化一手实战经验！
