
摘要
许多科学和工程中的数值算法都要求解稀疏三角矩阵线性系统。因此,研究者在各种高性能计算平台上对此进行了大量实验研究。一般来说,对于给定的问题,有几种不同的策略,此时很难判断哪一个是最优策略。因此,为每个矩阵选择最佳求解器(SPTRSV)的自动程序可以带来很大的性能收益。
本文依靠机器学习来预测每个矩阵的最佳SPTRSV程序,采用最高效的机器学习方法进行训练和预测。并在现有数据集的基础上,以人工生成的方式扩展数据集。并提出一些启发式方法来计算一些开销较大的特征的近似值。实验结果表明,该算法在不影响结果的前提下,大大提高了算法的运行效率。
1.简介
求解线性方程组的数值解通常要将原问题分解成三角形因子。因此,稀疏三角形线性方程组的解是稀疏数值线性代数中重要的组成部分之一。
近年来,几乎所有相关并行平台都实现了SPTRSV内核。然而,在这个特定的操作中产生的数据依赖使高效并行程序的设计变得复杂。另外,该操作计算强度低,数据访问模式不规则,很难获得较高性能。自从GPU被采用为通用HPC硬件以来,人们为各种平台提供高性能的SPTRSV实现做出了大量努力。其中最成功的两个案例是level-set和self-schedule范式。资料显示,这两种范式都是分别适合于某些特定线性系统。因此,矩阵属性成为选择求解器的重要因素,根据矩阵属性,可以预测哪个求解器或范例为给定的问题提供最小的执行时间。本文探讨了10个不同的矩阵特征对所选分类器的影响,研究了它们使用不同数据集的预测质量。实验评估显示,一些程序能够获得精度值为80%的预测。
2.稀疏三角线性系统的并行解
考虑线性系统Lx = b,其中L∈Rn×n是一个三角矩阵,b∈Rn是一个向量,x∈Rn是该问题的解。通常,稀疏矩阵L以某种稀疏存储格式存储,其中最常见的是CSR (Compressed Sparse Row)。在稀疏矩阵中,由于不规则的数据访问模式和低计算强度的共同影响,在SPTRSV中达到高水平的性能是一项具有挑战性的任务。此外,由于三角形系统的问题具有数据依赖和负载不平衡的特点,使得操作的并行化相当具有挑战性。随着HPC采用GPU等大规模并行处理器,对SPTRSV并行性的开发激发了大量的研究工作。不同研究人员进行实验分析,发现对于某一特定求解器而言,在一些线性系统上性能较高,但对其他线性系统性能较低。考虑到之前文献中给出的数值计算以及广泛使用的软件库的集成,最成功的例程主要有两种方法,level-set和self-scheduling,作者在之前的工作中详细描述了这两种策略,并研究了CSR稀疏矩阵格式中每种范式的一些最佳实现。本文对cuspv1例程(最具代表性的level-set策略实现)与self-scheduling的变体sf_nan、sf_order和sf_mr进行了比较。
3.自动选择
本文依赖于Matlab中的分类学习者应用程序,以获得用于确定最佳SPTRSV实现的有监督机器学习模型。Matlab模块包括5种技术,即决策树,判别分析,支持向量机,K近邻,和集成分类器。按照这条思路,本文考虑矩阵的10个特征:算术精度(prec)、矩阵维数(n)、非零个数(nnz)、最大每行非零个数(nnzmax)、平均每行非零个数(nnzavg)、每行非零标准差(nnzstdev)、平均带宽(bwavg)
、level-sets个数(level)、局部性 (locality)、多行局部性 (localitymr)。如前所述,不同特征的计算成本不同。其中,n、nnz、nnzavg可以从稀疏矩阵数据结构中以O(1)的代价得到,计算nnzmax、nnzstdev、bwavg和locality的代价为O(n),其中n为矩阵的维数。此外,level和localitymr的计算需要在sf_order或sf_mr变量的分析阶段之中或之后进行,其计算成本与线性系统的解阶段相似。因此,可以提取成本较低的特征来训练模型并评估模型的性能。在选择这些特征之后,本文训练了一组可用的机器学习模型,并执行了5折交叉验证,以估计训练模型在未见数据集上的准确性。本文使用数据集进行初步评估的结果如表1所示。可以看出,决策树分类器似乎是表现最好的分类器组,特别是考虑模型的训练和预测速度的情况下。K近邻分类器提供了一个合理的准确率,其中Fine KNN达到了74%的准确率,但预测速度较慢。相比之下,加权KNN具有相同的精度和更快的预测速度。一些集成分类器也显示出良好的准确性,尽管它们的预测速度比决策树和加权KNN分类器要慢。而判别分析分类器和支持向量机表现不佳。表 1. 分类器中包含的模型的准确性、预测速度和训练时间
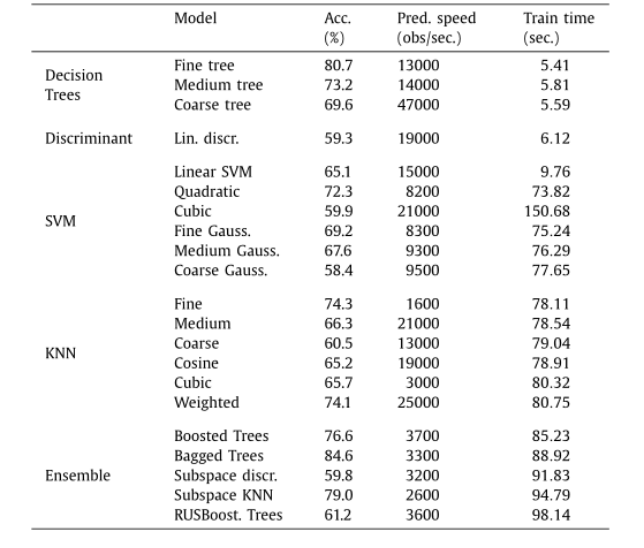
为了进行更详尽的评估,文章接下来关注决策树中表现最好的模型以及K近邻中表现最好的模型wKNN,考虑其准确性和预测速度之间的权衡。
4.实验评估
4.1硬件平台
在配备Intel Xeon Gold 6138 CPU(20核,2.00 GHz)和128 GB RAM的服务器上,对机器学习方法数据集中包含的线性系统的SPTRSV变量进行运行时评估,该服务器连接一个具有12 GB RAM的NVIDIA P100 GPU。操作系统为CentOS Linux 7(Core),用于GPU的CUDA工具包为9.2版本。 4.2初始数据集
为了进行实验评估,本文从Suite Sparse Matrix Collection中选择了一组中、大规模实数方阵,考虑总共981个稀疏方阵的下三角部分,维数n在1916到55042369之间,并且达到1.13亿个非零矩阵。除了前文所述的三角求解器外,实验还添加了两个与cuSprase库的最新版本cuspv2和cuspv2nl捆绑在一起的求解器。文章使用IEEE浮点表示法,在所有的实验中都是双精度的。4.3实验结果
针对前文的实验,文章选择了初始结果更好的分类方法来进行完整的分析,对决策树和wKNN方法在训练或预测的准确性和速度之间提供了一个很好的折衷。对于决策树,文章以最大深度100训练模型,并以基尼系数作为分割准则。加权KNN的训练使用欧几里德距离,距离的平方倒数作为权重,k
取10个最近的邻居。在某些情况下,一些矩阵特征的计算成本可能会很高,这可能会使预测所获得的增益变得模糊。因此,考虑哪些特征对机器学习模型的准确性有更大的影响是很重要的。为了研究每个特征的影响,并评估如何在不显著影响模型准确性的情况下减少预测因子的数量,本文对矩阵特征进行了逐一排除和筛选。表2总结了排除一些特征在训练模型获得的准确性方面的影响。这些模型的准确性是通过对原始数据集进行5折交叉验证来计算的。表 2. 对经过训练的机器学习模型进行5折交叉验证后,所得准确度和平均运行时误差
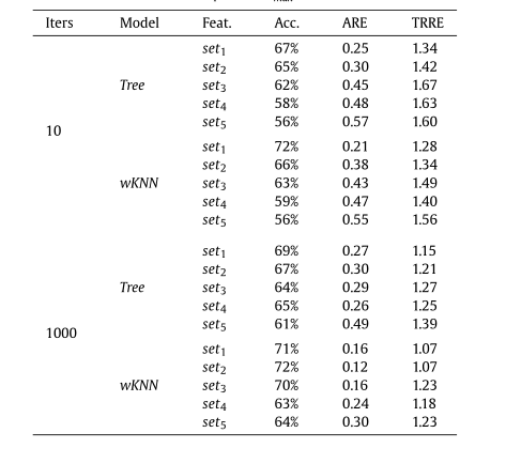
文章将计算的平均运行时错误(Average Runtime Error, ARE)定义为:总相对运行时误差(Total Relative Runtime Error, TRRE)定义为:其中Tpred为预测方法所占用的运行时间,Topt为最佳方法所需的运行时间,d为数据集中的观测数。ARE和TRRE的最佳值分别为0和1。
表2的结果表明,丢弃某些特征得到的效果是不均匀的。在某些情况下,删除某个特征会使结果变差,但有些情况下,会提高训练模型的准确性。实验表明,level和nnzmax/std特征对预测有更大的影响。对于决策树模型,在10次迭代的情况下,使用预测例程解决数据集中所有系统的运行时开销增加了19%,在1000次迭代的情况下增加了20%,而对于wKNN,当排除这些特性时,相应的开销增加了28%和17%。此外,排除nnzmax/std特征似乎对ARE有显著影响,而对TRRE的影响较小。这表明,对于相对较小的矩阵,行长度与求解器的性能相关性更强。
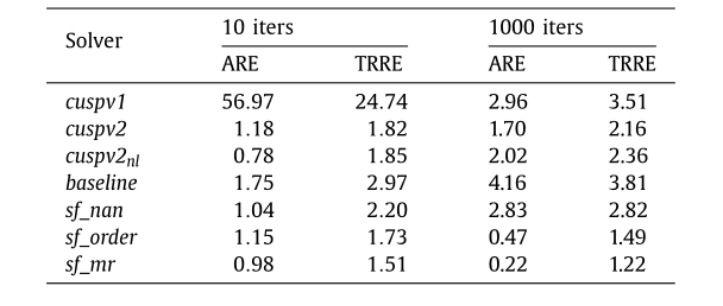
使用wKNN模型获得的最佳情况的TRRE表明,使用预测求解器处理整个数据集至少比使用10次迭代变量的最优算法多花28%的运行时间,比使用1000次迭代变量的最优算法多花7%的运行时间。然而,在表3中报告,在所有情况下使用相同的求解器会导致ARE和TRRE值相当差。事实上,使用sf_mr(通常是该数据集的最佳例程)至少比10次迭代和1000次迭代的最佳运行时分别多51%和22%。
表 3. 每个三角求解器求解整个数据集而获得的ARE和TRRE
5.提升策略
本文又从两个不同的方面扩展以前的工作,解决了减少特征计算所需的运行时间。文章使用一种启发式方法来估计隐含O(n)计算的特征。然后,通过使用一个稀疏矩阵生成程序对数据集进行扩展。5.1提高特征检测的速度
这项工作的目的是通过自动选择用于解决稀疏三角形线性系统问题的最佳求解器程序。为了使这一过程有效,机器学习模型仅仅预测准确是不够的,预测本身还要有尽可能少的开销。一般来说,由于训练阶段可以用于大量的问题,其开销可以忽略不计。因此整个过程的开销主要由两个方面组成:预测的计算成本,以及计算作为机器学习模型输入的矩阵特征所需的运行时间。
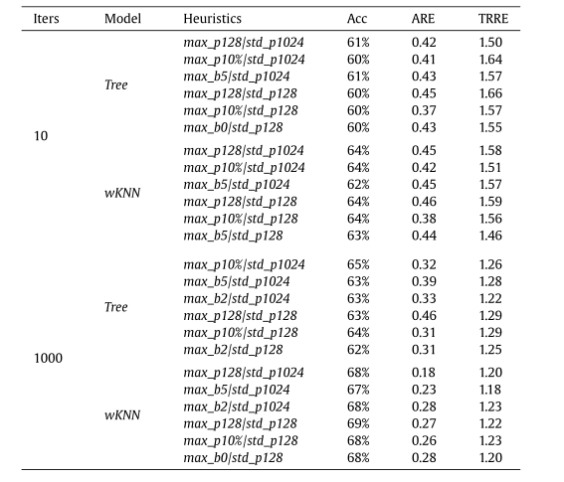
为了在计算过程中减少计算成本,文章研究了两种启发式方法:第一个是将行指针的向量划分为k个分区(n/k行)。对于每个分区,将计算每行非零的平均数目,并减少获得的值,同时保留最大值,该值将作为一行中估计的最大非零值返回。文章评估了这种启发式方法的三种变体所获得的结果:一种具有1024个分区(max_p1024),一种具有128个分区(max_p128),以及一种具有分区数量等于n的10% (max_p10%)。第二个启发式方法是递归二分搜索,在每一步中,将行分成两组,并在包含较多非零元素的组中继续递归。当分区只有一行时,该过程停止,返回该行的非零元素的数量。
表
4显示了使用set3特征训练的模型的精度结果,该过程将nnzmax和nnzstdev替换为启发式方法所得的近似值。结果表明,使用近似值与表2中set3的结果相比并没有显著差异。考虑到启发式算法的准确性和计算成本之间的平衡,提出了启发式算法组合max_p128 / std_p128脱颖而出。事实上,这种组合对于所有测试用例都能获得高精度的结果,而计算成本比之前方法小得多。因此,本文使用启发式算法组合max_p128/std_p128。
表 4. 用不同启发式算法返回的近似值替换nnzmax和nnzstdev特征后的模型性能
5.2提高预测精度
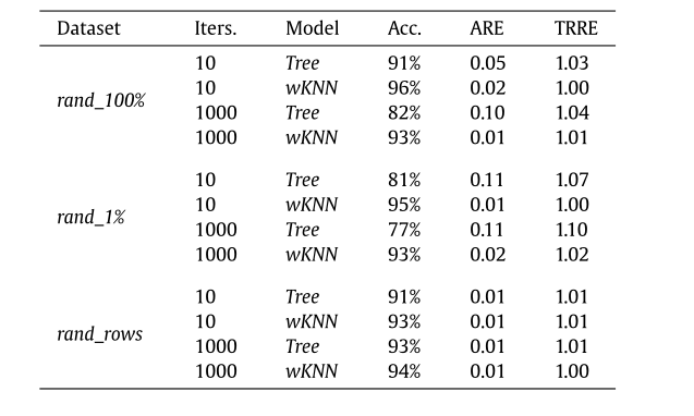
前面的实验中,用于训练的数据集由Suite Sparse Matrix Collection中的稀疏矩阵子集组成。但与机器学习应用程序的通常训练集相比,该集合中的稀疏矩阵的数量相当小。为了使用更大的训练集(数据扩充)进行计数,本文还进行了随机稀疏三角矩阵的生成,通过对原始矩阵进行随机扰动来创建新的矩阵。通过这种方式,我们希望生成更大的训练集,但同时保留在实际问题中发现的稀疏模式的一些特征。基于此方法,文章创建了三个随机数据集:(1)Rand_1%:只修改1%的非零条目的列索引。(2)Rand_100%:修改所有非零条目。(3)Rand_rows:修改所有的行和非零项。表5显示了使用wKNN和决策树模型对每个新数据集执行5倍交叉验证的结果。结果表明,模型在所有扩展数据集上都表现出了显著的性能,在大多数情况下准确率超过90%,ARE和TRRE可以忽略不计。表 5. 在扩展数据集max_p128/std_p128上使用交叉验证的模型性能
6.总结
本文提出了一个自动程序来选择一个给定的稀疏矩阵线性方程的最佳求解器。文章评估了不同的机器学习策略的性能。为了评估每个特征的重要性,在逐一去除这些特征的过程中测试它们的性能。为了提升特征检测速度,文章提出了启发式方法。最后为了提高准确性,通过对原始数据集进行随机扰动,生成更多的稀疏矩阵来构建更大的数据集进行实验。