点击上方“小白学视觉”,选择加"星标"或“置顶”
重磅干货,第一时间送达


随着人工智能尤其是深度学习的快速发展,计算机视觉成为了这些年特别热门的研究方向。在这里我们将开启一个全新的系列【计算机视觉那些事】,来分享我们这些年在计算机视觉上的一些认识和经验。在这个系列中,我们主要会围绕计算机视觉中的深度学习算法展开,包含图像分类、目标检测、图像分割和视频理解等诸多领域的理论和应用。
下面开始该系列的第一篇文章,在这篇文章中我们会对深度学习具体以深度神经网络为主的基础知识进行深入浅出的介绍,希望从零开始和大家一起一步步走进计算机视觉的世界。
在谈深度学习之前,我们首先来回顾一下感知机模型。感知机是深度神经网络的起源算法,学习和掌握感知机是通向深度学习的必经之路。
感知机是第一个从算法上完整描述的神经网络模型,也是应用于二分类任务的最简单的模型之一,模型的输入为样本的特征向量,输出为样本的类别,分别用 1 和 -1 表示。感知机的目标是将输入空间(特征空间)中的样本划分为正负两类分离的超平面,它的数学描述下式所示:
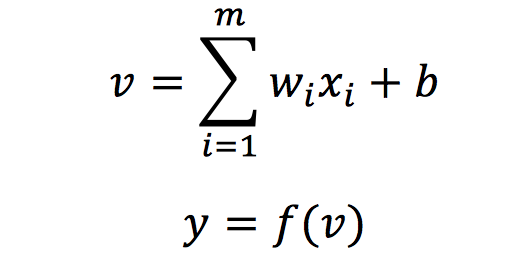
其中,wi表示输入样本的第i个特征xi所对应的权值,b表示模型具有的偏置量,f表示激活函数,这里使用sign阶跃函数,即大于0为1,其余为-1,y表示输入样本预测的标签。
在实际应用中,权值w和偏置b需要在训练过程中经过多次迭代来更新。为了便于表示,我们采用X来表示输入特征,W表示权值矩阵,将X和W改写为如下形式:
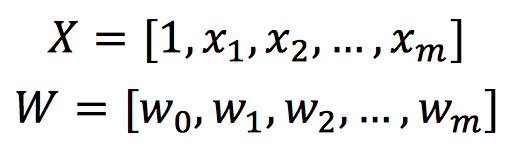
那么感知机就可以改写为
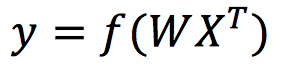
直观的计算流程如下图所示。
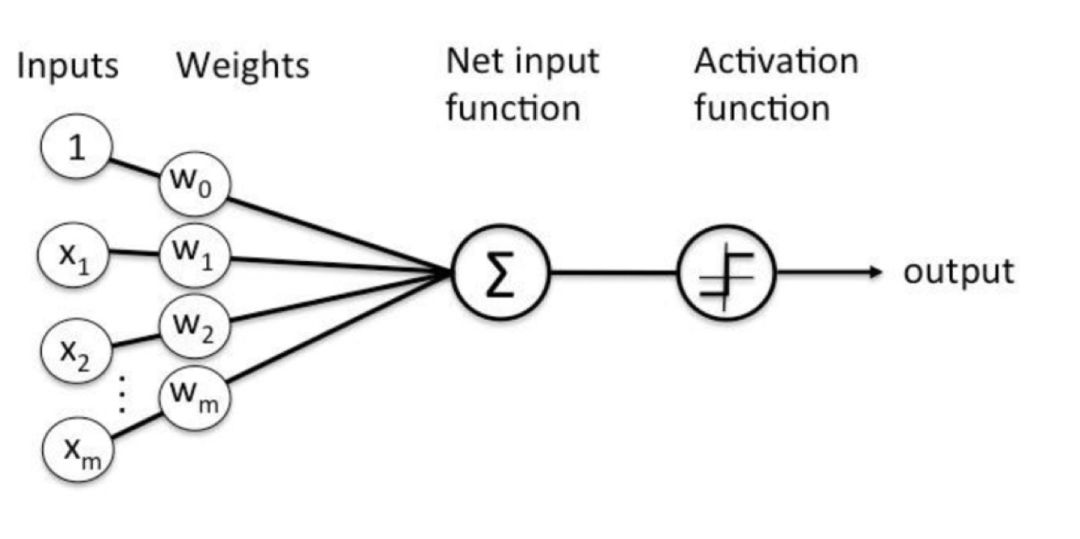
在感知机训练的过程中,我们针对分类错误的样本不断进行权值修正,逐步迭代直至最终分类符合预定标准,从而确定权值。具体地,我们一般采用基于误分类的损失函数,通过梯度下降算法来进行权值的更新,更新过程如下式所示:
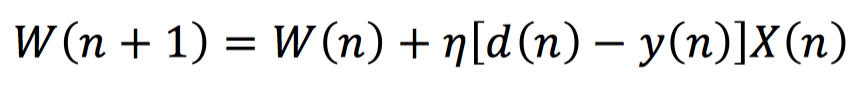
其中,d(n)表示第n次输入X(n)所对应的实际标签,y(n)表示第n次输入时感知机输出的预测标签,η表示学习率。
以图像二分类为例,假设我们已经有了每张图像的特征x和其对应的类别y,利用上述介绍的感知机就能够快速构建出一个图像二分类模型,然而感知机在分类过程中只能确定一个超平面,适合处理线性可分问题,但在复杂的非线性场景中并不擅长。
上一节我们介绍了处理简单二分类数据的单个感知机,在这一节中我们将从单个感知机过渡到多层感知机(MLP)。多层感知机是一种经典的神经网络模型,可以广泛地应用于复杂的非线性分类场景。下图展示了一个典型的多层感知机,也被称为全连接神经网络,其中每个蓝色的神经元代表一个感知机。
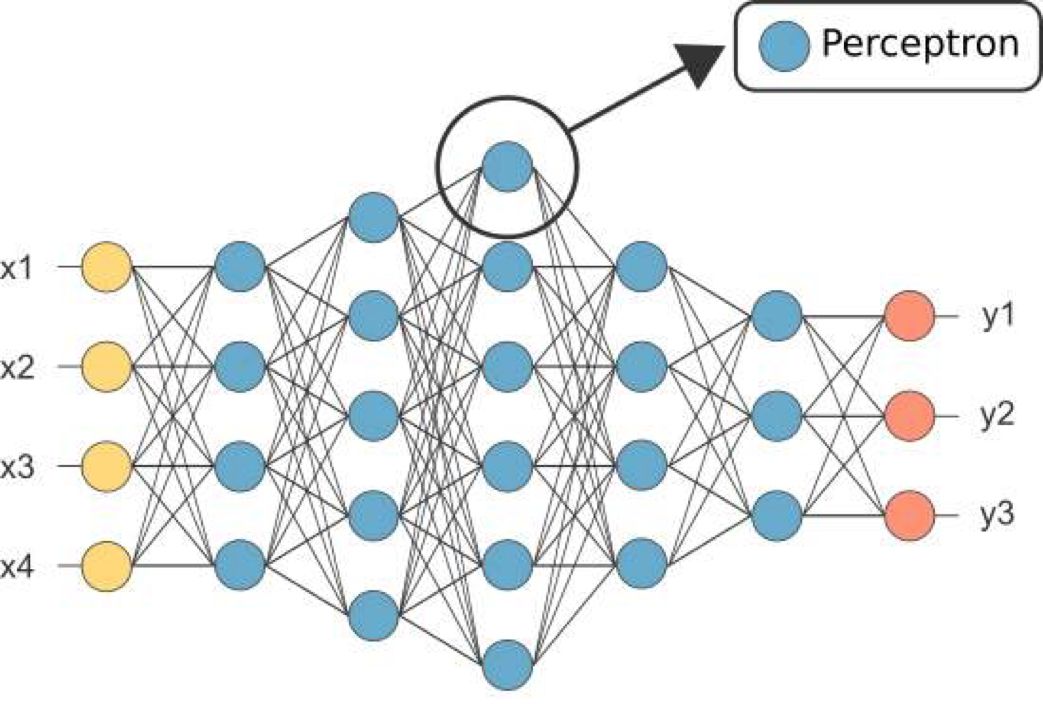
多层感知机将多个感知机(神经元)排列组成一个神经网络,与上一节介绍的感知机相比,增加了多个隐藏层,随着隐藏层数量的增加,模型的表达能力也不断增强,但同时也会增加网络的复杂度。此外,多层感知机可以有多个输出,这样模型可以灵活的应用于多分类任务。
在多层感知机中,每个神经元都会经过一个激活函数,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。试想一下如果没有激活函数每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这样的神经网络也就没有实际意义了。
多层感知机随着隐藏层数量的增加,使得网络最优权值的搜索空间变得很大。因此多层感知机的训练过程变得十分复杂。一般我们使用梯度下降来进行网络的训练,在训练过程中通过反向传播实现梯度的计算,其中包含两个阶段:
神经网络训练的基本流程如下:
1. 给定训练集同时设置学习率,并初始化网络连接中的所有权值;
2. 将训练集样本作为网络输入,计算网络输出值;
3. 根据损失函数计算网络输出值与实际标签值之间的误差;
4. 根据链式求导法则计算各个权重对输出误差的导数;
5. 根据梯度下降算法更新各个权值;
6. 重复2-5,直到达到收敛条件结束训练。
下面我们以一个具体的网络来展示多层感知机的前向和反向传播过程。
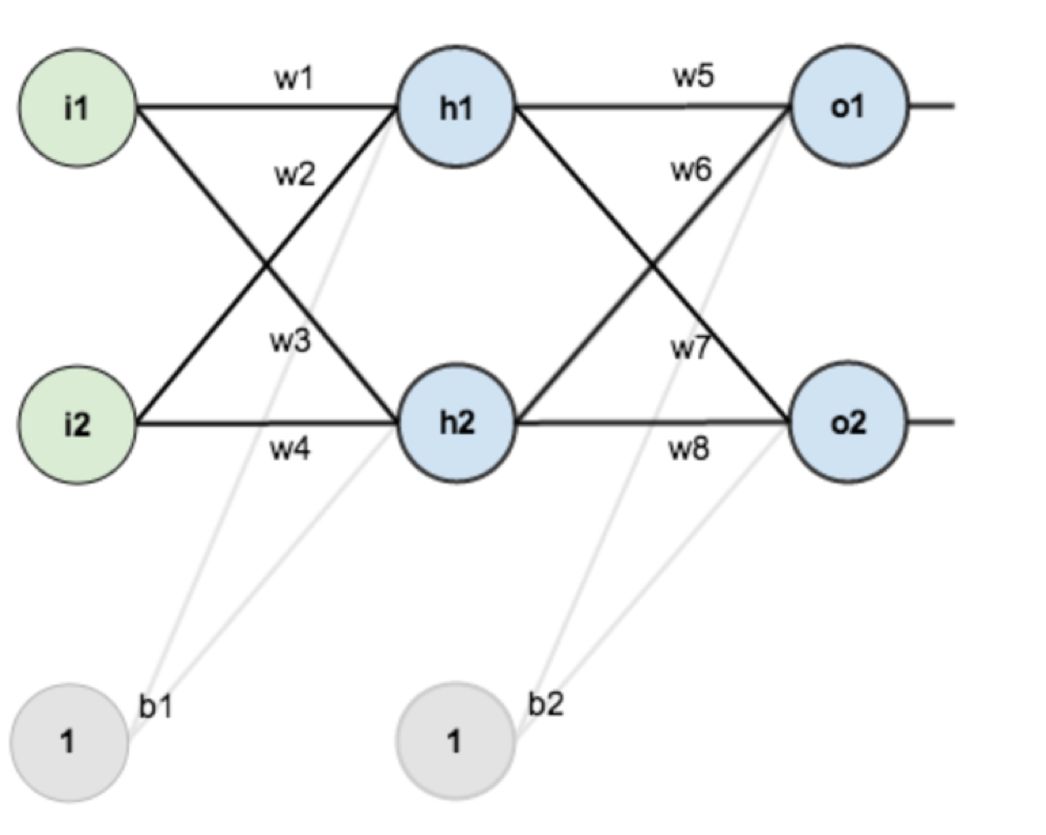
上图是一个两层神经网络,输入为i1和i2,输出为o1和o2。
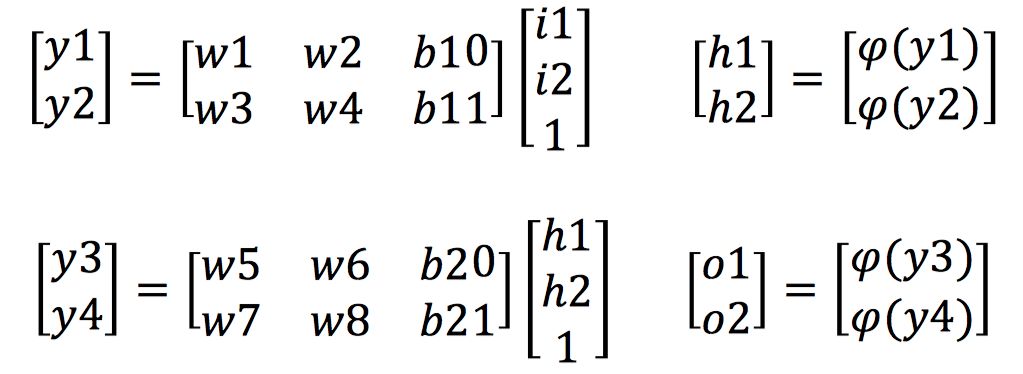
上面的式子展示了网络前向传播的计算过程,那么反向传播的过程是什么样呢?在这之前我们首先介绍反向传播的核心链式法则。链式法则是求取复合函数导数的一个法则,对于一个复合函数f(g(x)),它对x的导数可以由以下方式计算得到:
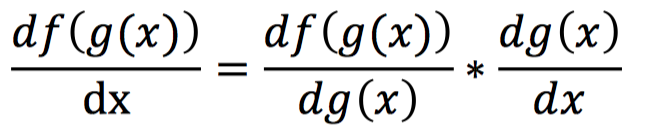
对于一个复合函数z=f(u,v),其中u=h(x,y),v=g(x,y),那么z对x和y的导数计算如下:
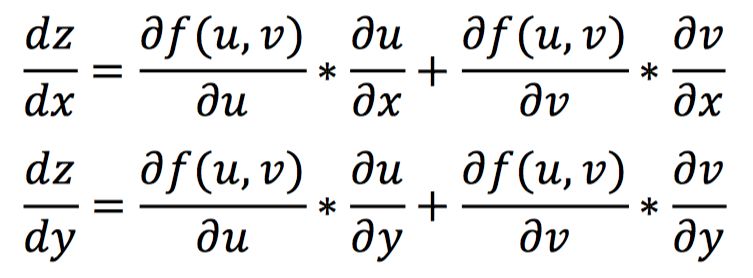
在熟悉了链式法则后,我们开始计算在反向传播中各权值的梯度。我们假设o1和o2输出端的梯度分别为g0和g1。首先根据链式法则我们可以计算出从输出到w5,w6和b20的梯度如下所示:
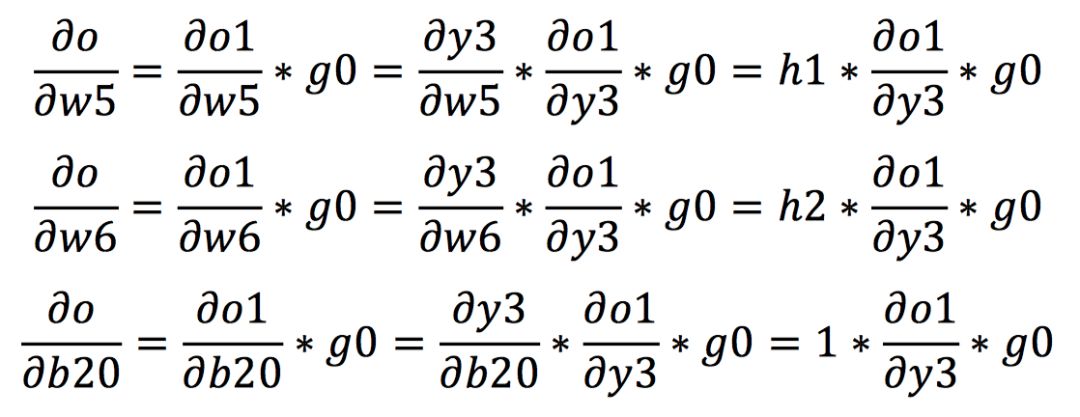
同理,我们可以进一步通过链式法则计算出从输出到网络的其他权值的梯度如下所示:
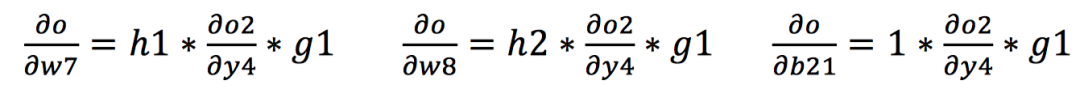
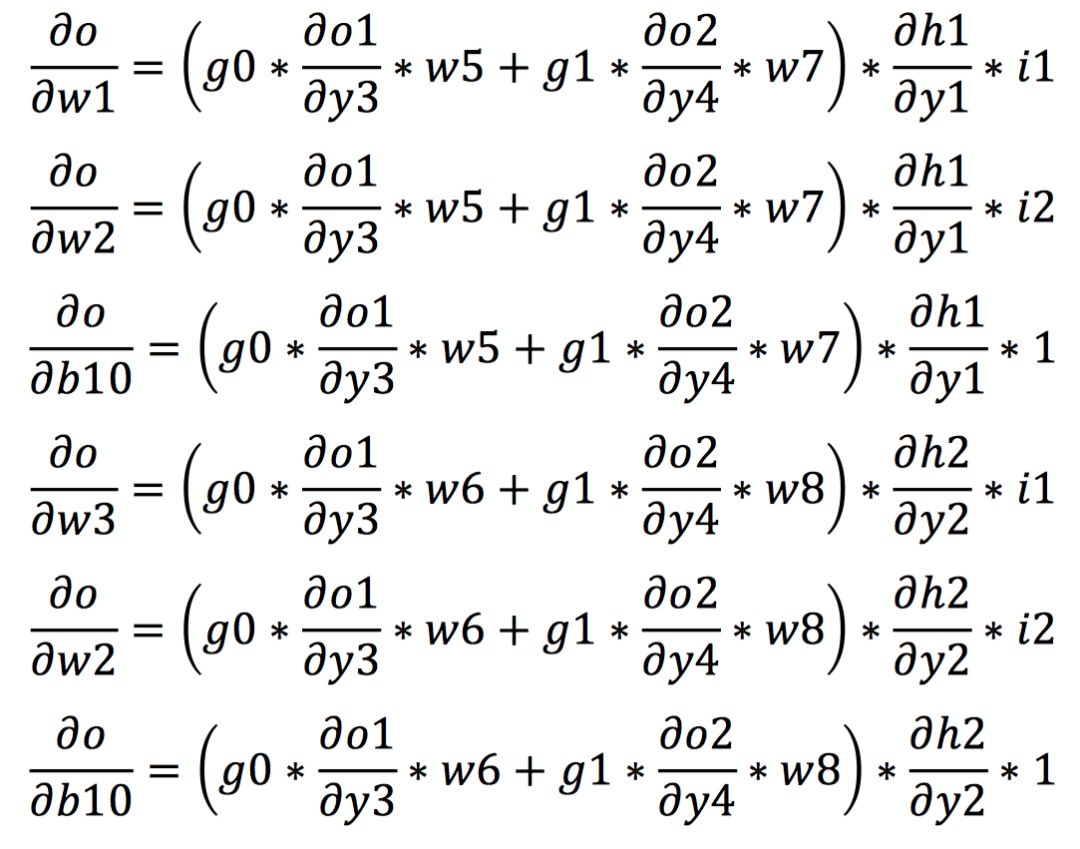
得到各个权值的梯度之后,我们再进一步根据梯度下降算法对权值进行计算,从而实现权值的更新。
在上面介绍的内容中,我们都多次提到激活函数。激活函数的使用让神经网络变得更加强大,能够表示输入输出之间非线性的复杂任意函数映射。在感知机的介绍中我们已经提到了sign激活函数,在这一节中我们将介绍更常用的三种激活函数Sigmoid、tanh和ReLU。
Sigmoid激活函数,数学表示和对应的导数形式如下:
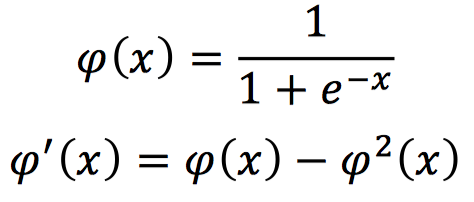
该激活函数的输出在0-1之间,在输入为较大的正值时,输出为1;输入为较小的负值时,输出为0。
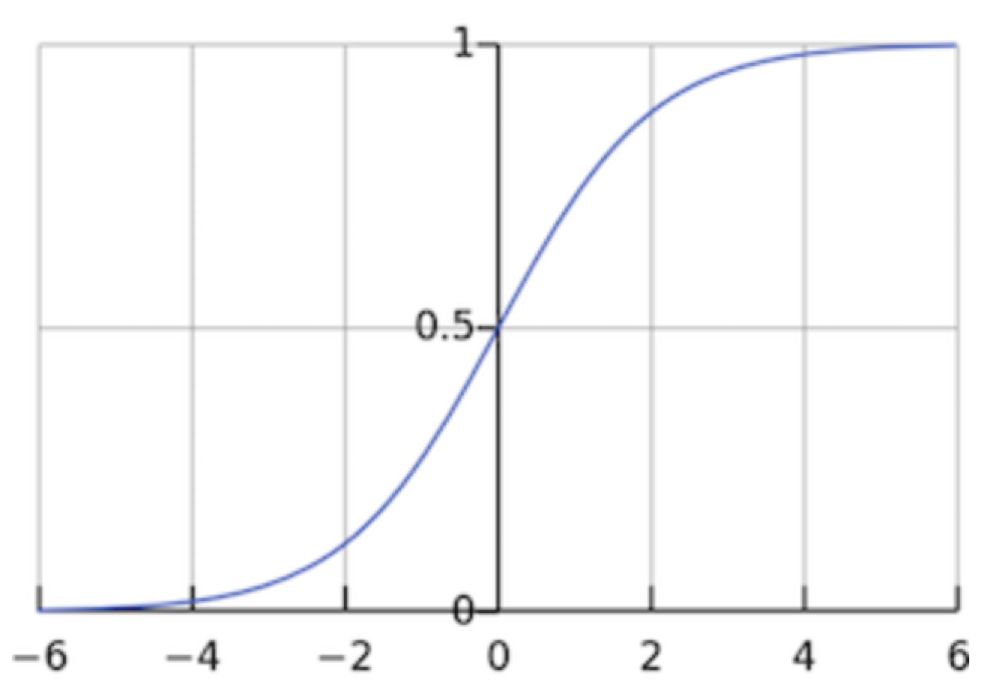
此外,由于它的导数在0-0.25之间,如果将这个激活函数应用在深度神经网络中,前向传播经过一次Sigmoid激活层,反向传播时,其梯度的衰减的最小值都为0.25,当采用多个Sigmoid激活函数时,其反向梯度会接近为0,这很容易导致梯度消失的情况出现。
tanh激活函数,数学表示和对应的导数形式如下:
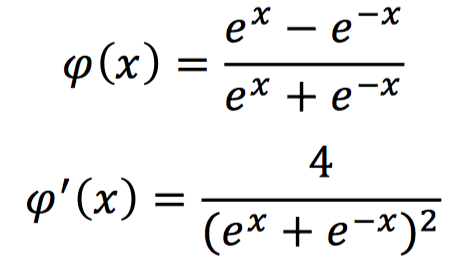
该激活函数的输出为-1到1之间的连续值,在输入为特别大的正值时,输出为1;输入为较小的负值时,输出为-1。
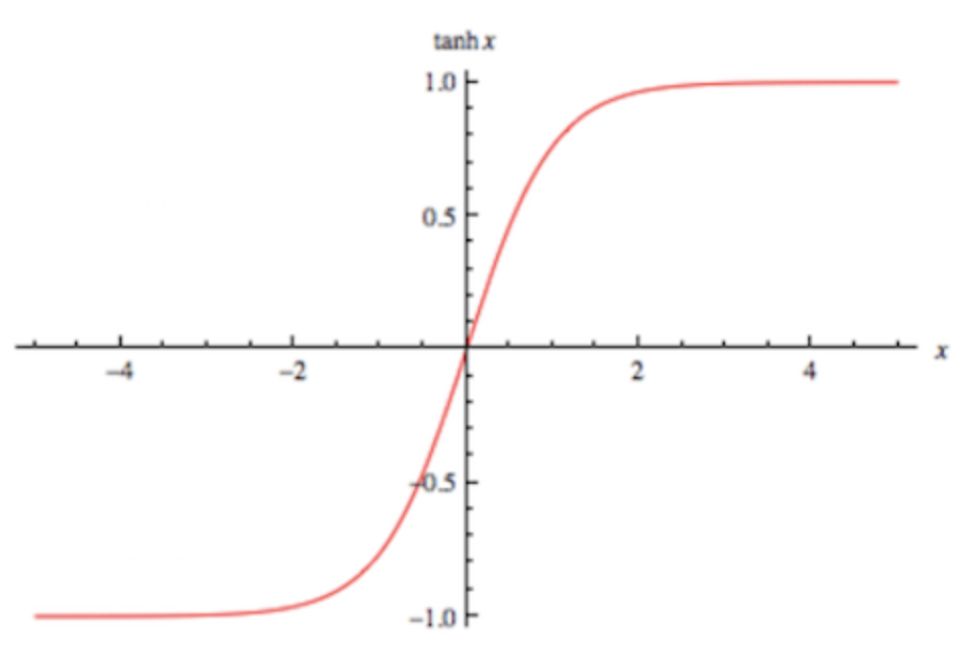
由其导数表达式可知,该激活函数的梯度最大值为1,分布在0到1之间。输入的值越偏离0,其梯度越小,所以仍旧存在梯度消失的问题。
ReLu激活函数,数学表示和对应的导数形式如下:
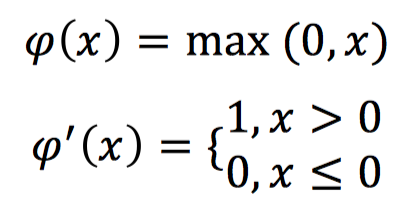
ReLU激活函数在输入大于0的时候导数为1,这种情况下则不会出现梯度消失的问题。
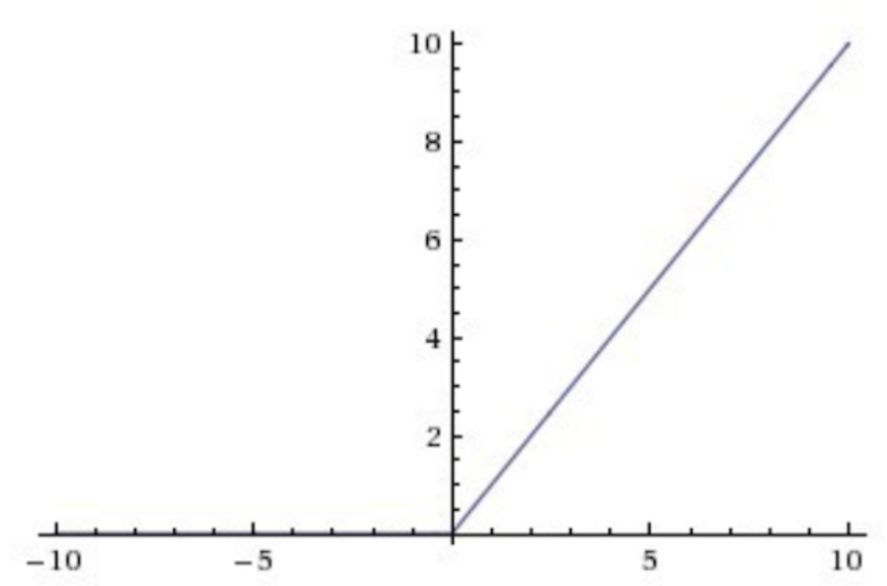
同时与指数运算的Sigmod和tanh相比,ReLU的计算量大大减少,所以ReLU当前被广泛应用于各式各样的深度神经网络中。然而当输入小于0时其导数为0,反向传播过程中不会进行梯度更新,可能会出现部分神经元永远不激活的情况。
上面列出了最为常见的三种激活函数,近些年还出现了不少性能优越的激活函数,在后续的文章中我们会一一介绍。在实际应用中,激活函数通常关系到网络的性能,所以要仔细选取使用。
我们从基本的神经网络开始,介绍了从单个感知机到多层感知机(MLP),从前向传播到反向传播,以及常用激活函数的相关内容。
在下一篇文章中,我们将会进一步从MLP过渡到卷积神经网络(CNN),同时也会介绍常见的梯度下降优化算法和损失函数。我们希望通过对神经网络基础知识的介绍,让大家能够更好地开启丰富多彩的计算机视觉之旅。
下载1:OpenCV-Contrib扩展模块中文版教程
在「小白学视觉」公众号后台回复:扩展模块中文教程,即可下载全网第一份OpenCV扩展模块教程中文版,涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。
在「小白学视觉」公众号后台回复:Python视觉实战项目,即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目,助力快速学校计算机视觉。在「小白学视觉」公众号后台回复:OpenCV实战项目20讲,即可下载含有20个基于OpenCV实现20个实战项目,实现OpenCV学习进阶。交流群
欢迎加入公众号读者群一起和同行交流,目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群(以后会逐渐细分),请扫描下面微信号加群,备注:”昵称+学校/公司+研究方向“,例如:”张三 + 上海交大 + 视觉SLAM“。请按照格式备注,否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告,否则会请出群,谢谢理解~

