深度学习用于异常检测，效果还是相当牛逼的。信用卡欺诈数据集，在孤立森林上能做到26%的top1000准确率，但是在Autoencoder算法上，最高做到了33.6%，但是这个数据很不稳定，有时候只有25%左右，但是至少这个模型潜力巨大，需要更多的试验，找到更稳定的网络结构。

自编码器（AutoEncoder, AE）是一类在半监督学习和非监督学习中使用的人工神经网络，其功能是通过将输入信息作为学习目标，对输入信息进行表征学习（representation learning），自编码器包含编码器（encoder）和解码器（decoder）两部分。

AutoEncoder是深度学习的一个重要内容，并且非常有意思，神经网络通过大量数据集，进行end-to-end的训练，不断提高其准确率，而AutoEncoder通过设计encode和decode过程使输入和输出越来越接近，是一种无监督学习过程，可以被应用于降维（dimensionality reduction）和异常值检测（anomaly detection），包含卷积层构筑的自编码器可被应用于计算机视觉问题，包括图像降噪（image denoising）、神经风格迁移（neural style transfer）等，本文主要讲解如何利用AutoEncoder进行异常检测试验。

用AutoEncoder进行降噪，可以看到通过卷积自编码器，我们的降噪效果还是非常好的，最终生成的图片看起来非常顺滑，噪声也几乎看不到了。

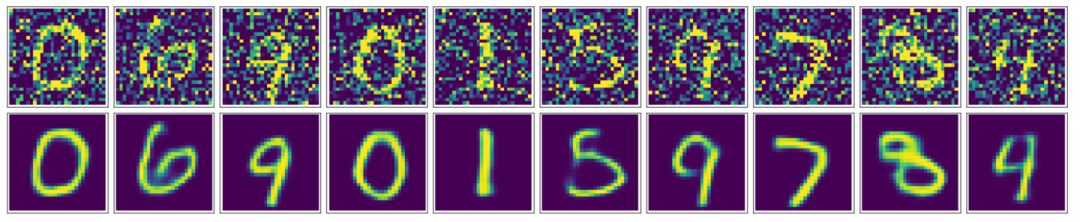
用AutoEncoder进行降维。

一、Autoencoder结构简介

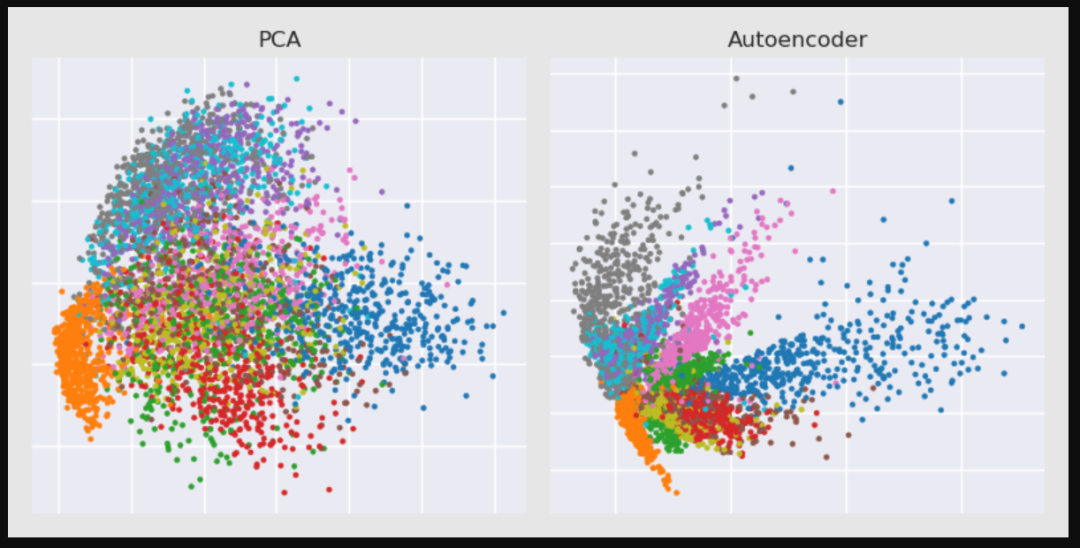
Autoencoder本质上它使用了一个神经网络来产生一个高维输入的低维表，Autoencoder与主成分分析PCA类似，但是Autoencoder在使用非线性激活函数时克服了PCA线性的限制。

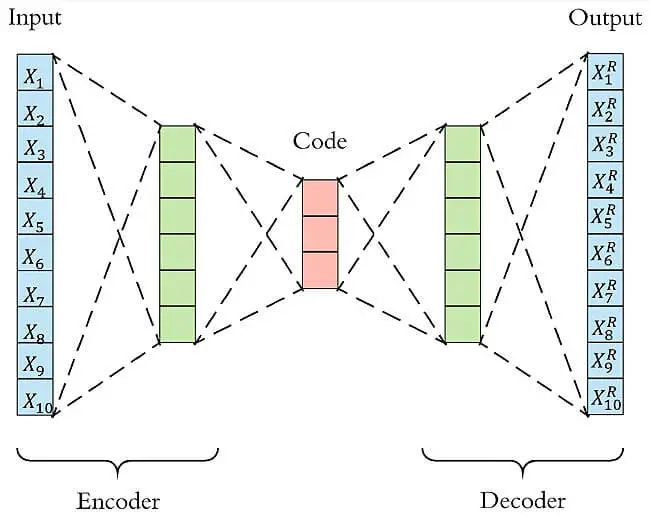
Autoencoder包含两个主要的部分，encoder（编码器）和 decoder（解码器）。Encoder的作用是用来发现给定数据的压缩表示，decoder是用来重建原始输入。在训练时，decoder 强迫 autoencoder 选择最有信息量的特征，最终保存在压缩表示中。最终压缩后的表示就在中间的coder层当中。

以下图为例，原始数据的维度是10，encoder和decoder分别有两层，中间的coder共有3个节点，也就是说原始数据被降到了只有3维。Decoder根据降维后的数据再重建原始数据，重新得到10维的输出。从Input到Ouptut的这个过程中，autoencoder实际上也起到了降噪的作用。

二、Autoencoder异常检测流程

异常检测(anomaly detection)通常分为有监督和无监督两种情形。在无监督的情况下，我们没有异常样本用来学习，而算法的基本上假设是异常点服从不同的分布。根据正常数据训练出来的Autoencoder，能够将正常样本重建还原，但是却无法将异于正常分布的数据点较好地还原，导致还原误差较大。

如果样本的特征都是数值变量，我们可以用MSE或者MAE作为还原误差。例如上图，如果输入样本为

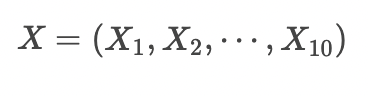
经过Autoencoder重建的结果为

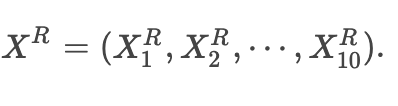
还原误差MSE为

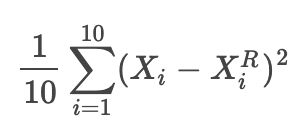
还原误差MAE为

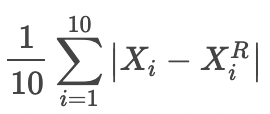
三、模型算法过程

数据还是使用信用卡的数据，数据来自于kaggle上的一个信用卡欺诈检测比赛，数据质量高，正负样本比例非常悬殊，很典型的异常检测数据集，在这个数据集上来测试一下各种异常检测手段的效果。当然，可能换个数据集结果就会有很大不同，结果仅供参考。

1、数据集介绍

信用卡欺诈是指故意使用伪造、作废的信用卡，冒用他人的信用卡骗取财物，或用本人信用卡进行恶意透支的行为,信用卡欺诈形式分为3种：失卡冒用、假冒申请、伪造信用卡。欺诈案件中，有60%以上是伪造信用卡诈骗，其特点是团伙性质，从盗取卡资料、制造假卡、贩卖假卡，到用假卡作案，牟取暴利。而信用卡欺诈检测是银行减少损失的重要手段。

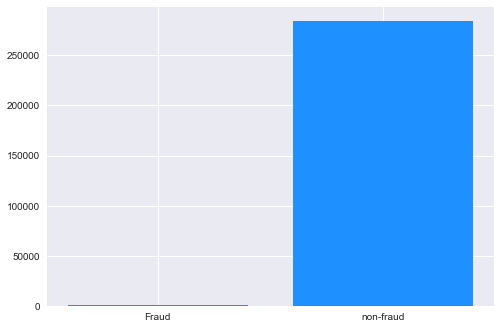
该数据集包含欧洲持卡人于 2013 年 9 月通过信用卡进行的交易信息。此数据集显示的是两天内发生的交易，在 284807 笔交易中，存在 492 起欺诈，数据集高度不平衡，正类（欺诈）仅占所有交易的 0.172%。原数据集已做脱敏处理和PCA处理，匿名变量V1， V2， ...V28 是 PCA 获得的主成分，唯一未经过 PCA 处理的变量是 Time 和 Amount。Time 是每笔交易与数据集中第一笔交易之间的间隔，单位为秒；Amount 是交易金额。Class 是分类变量，在发生欺诈时为1，否则为0。项目要求根据现有数据集建立分类模型，对信用卡欺诈行为进行检测。

注：PCA - "Principal Component Analysis" - 主成分分析，用于提取数据集的"主成分"特征，即对数据集进行降维处理。

2、数据来源

数据集 Credit Card Fraud Detection 由比利时布鲁塞尔自由大学(ULB) - Worldline and the Machine Learning Group 提供。可从Kaggle上下载：https://www.kaggle.com/mlg-ulb/creditcardfraud

自己下载数据

3、模型搭建

需要的包比较多，我们先加载下

# 加载所需要的包import warningswarnings.filterwarnings("ignore")import os import pandas as pd import numpy as np import matplotlib.pyplot as plt#plt.style.use('seaborn')import tensorflow as tfimport seaborn as snsfrom sklearn.model_selection import train_test_splitfrom keras.models import Model, load_modelfrom keras.layers import Input, Dense,LeakyReLU,BatchNormalizationfrom keras.callbacks import ModelCheckpointfrom keras import regularizersfrom sklearn.preprocessing import StandardScalerfrom sklearn.metrics import roc_curve, auc, precision_recall_curve# 工作空间设置os.chdir('/Users/wuzhengxiang/Documents/DataSets/CreditCardFraudDetection')os.getcwd()

数据读取和简单的特征工程

# 读取数据d = pd.read_csv('creditcard.csv')
# 查看样本比例num_nonfraud = np.sum(d['Class'] == 0)num_fraud = np.sum(d['Class'] == 1)plt.bar(['Fraud', 'non-fraud'], [num_fraud, num_nonfraud], color='dodgerblue')plt.show()
# 删除时间列，对Amount进行标准化data = d.drop(['Time'], axis=1)data['Amount'] = StandardScaler().fit_transform(data[['Amount']])X = data.drop(['Class'],axis=1)Y = data.Class

模型搭建+模型训练

# 设置Autoencoder的参数input_dim    = X.shape[1]encoding_dim = 128num_epoch    = 30batch_size   = 256
input_layer = Input(shape=(input_dim, ))
encoder = Dense(encoding_dim,                 activation="tanh",                 activity_regularizer=regularizers.l1(10e-5)                )(input_layer)encoder =BatchNormalization()(encoder)encoder=LeakyReLU(alpha=0.2)(encoder)
encoder = Dense(int(encoding_dim/2),                 activation="relu"                )(encoder)encoder =BatchNormalization()(encoder)encoder=LeakyReLU(alpha=0.1)(encoder)
encoder = Dense(int(encoding_dim/4),                 activation="relu"                )(encoder)encoder =BatchNormalization()(encoder)





    
### decoderdecoder = LeakyReLU(alpha=0.1)(encoder)decoder = Dense(int(encoding_dim/4),                activation='tanh'                )(decoder)decoder = BatchNormalization()(decoder)decoder = LeakyReLU(alpha=0.1)(decoder)

decoder = Dense(int(encoding_dim/2),                activation='tanh'                )(decoder)decoder = BatchNormalization()(decoder)decoder = LeakyReLU(alpha=0.1)(decoder)
decoder = Dense(input_dim,                 #activation='relu'                )(decoder)
autoencoder = Model(inputs = input_layer,                     outputs = decoder                    )autoencoder.compile(optimizer='adam',                     loss='mean_squared_error',                     metrics=['mae','mse']                    )
# 模型保存为 XiaoWuGe_model.h5，并开始训练模型checkpointer = ModelCheckpoint(filepath="XiaoWuGe_model.h5",                               verbose=0,                               save_best_only=True                               )history = autoencoder.fit(X,                           X,                          epochs=num_epoch,                          batch_size=batch_size,                          shuffle=True,                          #validation_data=(X_test, X_test),                          verbose=1,                           callbacks=[checkpointer]                          ).historyEpoch 1/30284807/284807 [==============================] - 39s 136us/step - loss: 0.6593 - mae: 0.3893 - mse: 0.4098Epoch 2/30Epoch 29/30284807/284807 [==============================] - 41s 144us/step - loss: 0.1048 - mae: 0.1188 - mse: 0.0558Epoch 30/30284807/284807 [==============================] - 39s 135us/step - loss: 0.0891 - mae: 0.1134 - mse: 0.0495


模型结果可视化
# 画出损失函数曲线plt.figure(figsize=(14, 5))plt.subplot(121)plt.plot(history['loss'], c='dodgerblue', lw=3)plt.title('model loss')plt.ylabel('mse')plt.xlabel('epoch')plt.legend(['train'], loc='upper right')

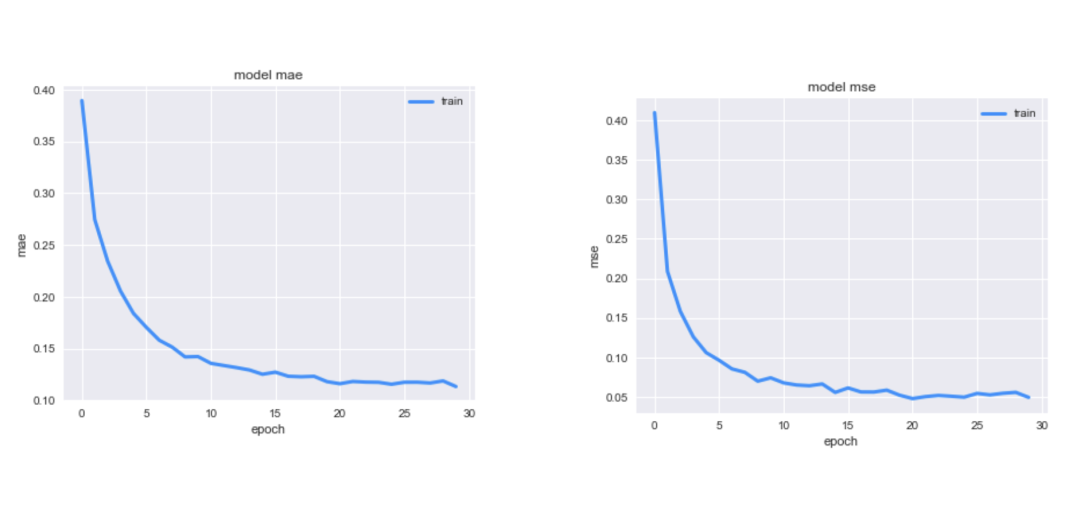
# 画出损失函数曲线plt.figure(figsize=(14, 5))plt.subplot(121)plt.plot(history['mae'], c='dodgerblue', lw=3)plt.title('model mae')plt.ylabel('mae')plt.xlabel('epoch')plt.legend(['train'], loc='upper right')
# 画出损失函数曲线plt.figure(figsize=(14, 5))plt.subplot(121)plt.plot(history['mse'], c='dodgerblue', lw=3)plt.title('model mse')plt.ylabel('mse')plt.xlabel('epoch')plt.legend(['train'], loc='upper right')

模型结果预测

#利用训练好的autoencoder重建测试集pred_X  = autoencoder.predict(X)# 计算还原误差MSE和MAEmse_X = np.mean(np.power(X-pred_X,2), axis=1)mae_X = np.mean(np.abs(X-pred_X),     axis=1)

data['mse_X'] = mse_Xdata['mae_X'] = mae_X# TopN准确率评估n = 1000df =  data.sort_values(by='mae_X',ascending=False)df = df.head(n)rate = df[df['Class']==1].shape[0]/nprint('Top{}的准确率为:{}'.format(n,rate))
Top1000的准确率为:0.336

可以看到，我们的准确率为0.336，比之前的孤立森林又有了很大的提高，但是我经过了比较多的试验，这是比较理想的结果。后期我会找个更加稳定的结构分享给大家，下面我可以可以看看，正样本和负样本的一个分布差异。

# 提取负样本，并且按照7:3切成训练集和测试集mask = (data['Class'] == 0)X_train, X_test = train_test_split(X, test_size=0.3,                                   random_state=520)
# 提取所有正样本，作为测试集的一部分X_fraud = X[~mask]

# 利用训练好的autoencoder重建测试集pred_test  = autoencoder.predict(X_test)pred_fraud = autoencoder.predict(X_fraud)

# 计算还原误差MSE和MAEmse_test = np.mean(np.power(X_test - pred_test, 2), axis=1)mse_fraud = np.mean(np.power(X_fraud - pred_fraud, 2), axis=1)mae_test = np.mean(np.abs(X_test - pred_test), axis=1)mae_fraud = np.mean(np.abs(X_fraud - pred_fraud), axis=1)mse_df = pd.DataFrame()mse_df['Class'] = [0] * len(mse_test) + [1] * len(mse_fraud)mse_df['MSE'] = np.hstack([mse_test, mse_fraud])mse_df['MAE'] = np.hstack([mae_test, mae_fraud])mse_df = mse_df.sample(frac=1).reset_index(drop=True)

# 分别画出测试集中正样本和负样本的还原误差MAE和MSEmarkers = ['o', '^']markers = ['o', '^']colors = ['dodgerblue', 'red']labels = ['Non-fraud', 'Fraud']
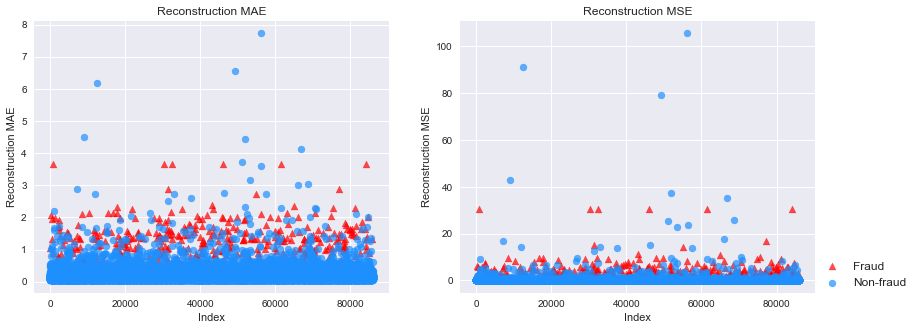
plt.figure(figsize=(14, 5))plt.subplot(121)for flag in [1, 0]:    temp = mse_df[mse_df['Class'] == flag]    plt.scatter(temp.index,                 temp['MAE'],                  alpha=0.7,                 marker=markers[flag],                 c=colors[flag],                 label=labels[flag])plt.title('Reconstruction MAE')plt.ylabel('Reconstruction MAE')plt.xlabel('Index')
plt.subplot(122)for flag in [1, 0]:    temp = mse_df[mse_df['Class'] == flag]    plt.scatter(temp.index,                 temp['MSE'],                  alpha=0.7,                 marker=markers[flag],                 c=colors[flag],                 label=labels[flag])plt.legend(loc=[1, 0], fontsize=12)plt.title('Reconstruction MSE')plt.ylabel('Reconstruction MSE')plt.xlabel('Index')plt.show()

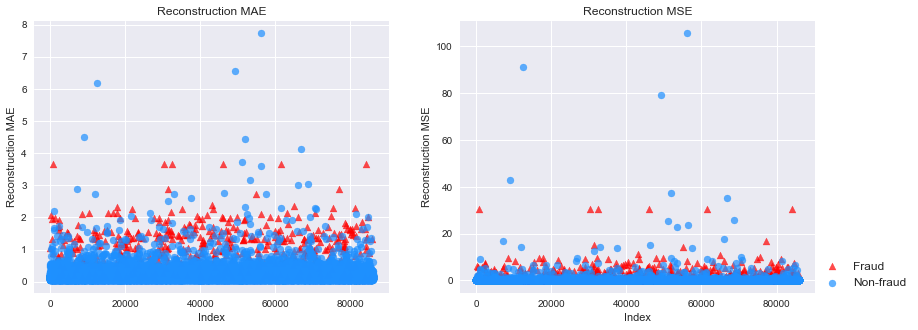
可以看到，正负样本的MAE和MSE有比较明显的差异，证明这个算法有很好的异常检测能力，当然，有部分正常样本还是很难通过异常检测分开。