优化｜深度学习或强化学习在组合优化方面有哪些应用？

来源：图灵人工智能

前言

深度强化学习求解组合优化问题近年来受到广泛关注，是由于其结合了强化学习(Reinforcement learning)强大的决策(decision-making)能力和深度学习(deep learning)的各种模型(RNN、Transformer、GNN等等)强大的信息提取表征能力(representative)，同时又结合神经网络强大的函数近似功能，可以采用神经网络近似Value-based RL中的Q值函数或V值函数，或者直接将其当作Policy-based RL中的策略(policy)。

三巨头之一的Yoshua Bengio在EJOR期刊上发表的文章( )对机器学习(Machine learning)用于组合优化(Combinatorial Optimization，CO)提出了三类范式：

NO.1 End-to-end ML for CO

采用机器学习算法端到端地求解组合优化问题，避免了传统优化算法的设计及其迭代效率低运算复杂度高等特点。此类方法能够学习问题本身的属性从而提升计算效率(例如传统的优化算法需要针对每个实例进行从头迭代计算，而机器学习算法可以通过训练的方式学习问题的共性特征从而直接将训练的模型进行部署测试(offline -> online))。再借助神经网络的并行计算能力，模型能够在极短的时间内给出优化方案。因此，该方法的优势是经过预训练(pre-training)的模型求解速度非常快、时间复杂度低的特点，适合一些需要进行实时优化的场景，如滴滴就将该方法用于在线打车调度平台。文章( )分析了所提出的End2end框架在求解路径问题时无论在训练(training)还是在测试（testing/inference）阶段都具有线性(O(N))运行时间复杂度，能够非常快速的给出一个次优解，相比于启发式算法和精确算法都有一定优势，在运行时间和求解精度上有一定的trade-off。

图1 End-to-end ML for CO

此类方法的难点是如何把一个复杂的优化问题建模为马尔科夫决策过程(Markov Decision Process, MDP)包括对环境的建模，对动作、状态、收益函数的定义。其核心问题是需要解决模型的泛化性能(generalization ability), 通常训练需要大量数据，如果训练数据的分布与应用场景的数据分布偏差很大就会存在较大的分布偏移(Distribution shift)，对于该问题作者感觉可以借鉴pre-training -> fine-tuning的思路。

答猪硕士期间的工作主要是围绕这类方法进行的(对routing problem & scheduling problem的研究, 下面有详细介绍及源码)，对于泛化问题的处理主要考虑的是对训练得到的模型进行Ensemble(即保存每个epoch的参数测试时取效果最好的模型，借助算力可以忽略运算时间的消耗)。

NO.2 Learning meaningful properties of optimization problems (i.e., integrating ML in OR methods), 将机器学习算法与传统的运筹优化方法进行结合

图2 The machine learning model is used to augment an operationresearch algorithm with valuable pieces of information.

NO.3 Machine learning alongside optimization algorithms

第二类和第三类都属于借助ML方法辅助运筹优化算法进行求解，如在解决一些精确算法中的子问题（分支定界算法中挑选variable的问题）。或者结合元启发式算法(meta-heuristics)，如在local search类算法中的邻域搜索算法，可以采用ML方法来挑选邻域结构。此外，动态调度类问题也常用到这类方法，如采用ML方法在每个动态调度决策点挑选合适的调度规则。

该类方法利用ML方法的学习表征能力帮助运筹优化算法进行决策，其底层任然属于传统优化算法的运行方式，不过结合ML方法可以提升搜索效率等。其优化结果的质量通常能够得到保障，但该方法的运算效率与端到端的ML方法不在同一量级。

图 3 The combinatorial optimization algorithm repeatedly queries thesame ML model to make decisions.

End-to-end ML for CO文献总结

第一篇该方向的论文是google的Vinyals大神提出的Pointer Network，该网络改编与NLP领域的Sequence-to-sequence模型，由于S2S模型是基于一个固定的词库进行输出, 即输入的维度与输出不对等(e.g., 输入10个词我是基于一个固定的词库(可能是一万个)进行采样输出)，对应于组合优化问题需要输出维度随着输入维度改变(e.g., 对于一个TSP问题，给定不同客户节点数量我需要输出对应数量的序列)，该论文基于这样的思路完成了S2S -> PN的改编，大体思路就是用一个encoder(i.e., MLP/RNN/CNN/GNN/Transformer etc.)对输入(node)进行embedding得到高维的embedding vectors（隐变量），decoder（i.e., attention-based RNN/Transformer/MLP etc.）基于该隐变量进行解码(一顿操作再过一个softmax得到与输入维度相同的一个概率分布(即对应RL中的policy))，然后基于该policy进行策略解码，可以是 random sampling、greedy、beam search或者是后面提出的active search等等。

后续的文章将强化学习与Pointer network进行结合->有作者认为大多数组合优化问题不存在时序信息因此将PN中的RNN替换为CNN(RNN不能并行计算，CNN可以并行计算效率更高)->KOOL 将Transformer结合RL用于求解组合优化问题->大量GNN的结合。

相关文章链接大家可以看其他回答的内容。

现在模型算法改不动了，大家好像又转向第2、3种范式了，如今年ICLR的一篇工作Learning Scenario Representation for Solving Two-stage Stochastic...；近期有篇arxiv的文章关于RL for branching的研究也很有意思(传送门：Reinforcement Learning for Branch-and-Bound Optimisation using Retrospective Trajectories)，作者认为以往采用模仿学习(imitation learning, IL)即行为克隆的方法来学习branch and bound的过程耗费人力物力(需要质量较高的专家轨迹)，因此作者将branching挑选variable的的过程建模为MDP，从而学到较优的policy完成这一过程。

相关的文章

作者使用深度强化学习求解组合优化问题（routing problem、scheduling problem）

1、Solve routing problems with a residual edge-graph attention neural network ；

文章链接：

https://www.sciencedirect.com/science/article/pii/S092523122200978X ；

开源代码地址：GitHub - leikun-starting/DRL-and-graph-neural-network-for-routing-problems

大多许多组合优化问题都基于图结构，可以很容易地通过现有的图嵌入或网络嵌入技术来建模，将图信息嵌入到连续的节点表示中。图神经网络的最新发展可以用于网络设计，因为它在信息嵌入和图拓扑的信念传播方面具有很强的能力。这激励我们采用图模型来建立End-to-end的深度强化学习框架。旨在设计近似求解图组合优化问题的通用框架，该框架应用于不同的图组合优化问题只需要做细微的改动，图1概述了该框架的流程。TSP和VRP作为两个经典的组合优化问题，已经在物流运输、遗传学、快递和调度领域得到了广泛的研究。论文以TSP和VRP为求解对象来验证所提通用框架的有效性。

一般而言，TSP定义在一个有多个节点的图上，需要搜索节点的排列，以查找具有最短行驶距离的最优解。带容量约束的车辆路径问题(capacitated vehicle routing problem, CVRP)是VRP的一个重要变体，其要求在不违反车辆容量限制的约束下，寻找行驶距离最短的路径，并满足所有客户的需求。由于TSP和CVRP的NP-hard性质，即使在二维欧几里得的情况下也很难找到最优解。一般来说，这样的NP-hard问题可以表示为图上的顺序决策任务，因为它具有高度结构化的性质。

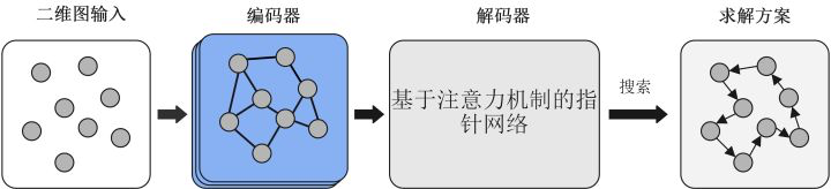
图4 所提出框架求解TSP的流程

本文设计的框架中，首先将问题的图表示(如TSP的节点坐标)输入到模型中，然后采用GNN对原始特征进行编码。在解码过程中，通过注意力机制预测未选择节点的概率。通过搜索策略基于该概率分布进行节点选择，如贪婪搜索或采样的解码策略。本文的编码器是对GAT的改编，改编版本考虑了图结构中的边信息和层之间的残差连接。本章将所设计的编码器网络称为残差-边-图注意力网络(residual edge graph attention network, RE-GAT)。除了对节点的原始状态进行编码外，RE-GAT还对边的信息进行编码更新。边的特征可以为学习策略提供与优化目标相关的更多的直接信息(如加权距离)。路径优化问题的目标是在相应的约束条件下寻找最短的加权路径，因为边提供的权重信息(本章选择图中节点之间的距离)不由节点提供。此外，同时输入节点和边缘信息有利于挖掘不同节点之间空间邻接关系的特征。本文的解码器是基于Transformer模型设计的。训练算法使用近端策略优化算法 (proximal policy optimization, PPO)和改进的REINFORCE算法。

所提出的框架无论在训练(training)还是在测试（testing/inference）阶段都具有线性(O(N))运行时间复杂度结合神经网络的批(batch)处理能力，能够非常快速的给出一个次优解，相比于启发式算法和精确算法都有一定优势，在运行时间和求解精度上属于trade-off。

具体方法实现和实验结论请参考原文链接。

2、A Multi-action Deep Reinforcement Learning Framework for Flexible Job-shop Scheduling Problem ；文章链接：https://www.sciencedirect.com/science/article/pii/S0957417422010624；开源代码地址：https://github.com/leikun-starting/End-to-end-DRL-for-FJSP ；https://github.com/leikun-starting/Dispatching-rules-for-FJSP

柔性作业车间调度问题作为典型的NP-hard组合优化问题，目前其求解方法主要分为两类：精确算法和近似算法。基于数学规划的精确算法可以在整个解空间中搜索以找到最优解，但这些方法由于其NP-hard特性难以在合理的时间内解决大规模调度问题。因此，越来越多的近似方法(包括启发式、元启发式和机器学习技术)用于求解大规模调度问题。通常，近似方法可以在计算时间和调度结果的质量之间实现良好的折中，特别是群体智能（swarm intelligence, SI）和进化算法（evolutionary algorithm, EA），如遗传算法、粒子群算法、蚁群算法、人工蜂群算法等。

尽管与精确算法相比，SI和EA可以在合理的时间内解决FJSP，但这些方法并不能直接应用于求解产线实时运行需求下的大规模资源调度问题。基于优先级的启发式调度规则被广泛地应用于实时调度系统，例如考虑动态事件的调度问题。调度规则通常具有较低的计算复杂度，并且比数学编程和元启发式算法更容易实现。通常，用于解决FJSP的调度规则可以分为两个基本类别：工件选择规则和机器选择规则。这些规则的设计和组合旨在最小化调度目标，例如平均完工时间、平均延误、最大延误。然而，有效的调度规则通常需要大量的领域专业知识和反复试验，并且不能保证求解质量。

近年来，深度强化学习 (deep reinforcement learning, DRL)已广泛地应用于求解组合优化问题，为解决具有共同特征的调度问题提供了一种思路。然而，目前的工作主要专注于其他类型的组合优化问题，例如旅行商问题和车辆路径问题，对于更为复杂的调度问题如FJSP研究较少。

通常，常规的强化学习仅适用于单个动作的决策问题。其中，强化学习智能体与环境交互的方式为：智能体首先从环境中获取状态并根据该状态选择动作，然后获得奖励并转移到下一个状态。然而，在FJSP 中面临着工序的排序任务和机器的指派任务，即该问题是一个具有多动作空间的决策问题，这意味着常规的强化学习不能直接应用于FJSP。图5构建了 FJSP 的多动作空间的层级结构。在该层级结构中，强化学习智能体首先从工序动作空间中选择一个工序动作，然后从机器动作空间中选择一个机器动作。

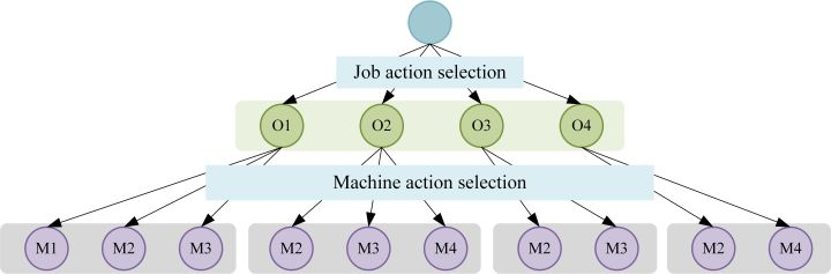
图5 FJSP的层级动作空间结构示意图

本文首先将柔性作业车间调度过程描述为多动作强化学习任务，并进一步将该任务定义为一个多马可夫决策过程(Multi-Markov Decision Process)。在此基础上，提出了一种新的基于GNN的多指针图网络(multi-pointer graph network, MPGN，如图6所示)用于编码嵌入FJSP的析取图(Disjunctive Graph)作为局部状态, 注：析取图作为调度过程中的局部状态提供了调度过程中的全局信息包含数值和结构信息，如工序优先级约束、调度后的工序在每台机器的加工顺序、每个工序的兼容机器集合以及兼容机器的加工时间等。

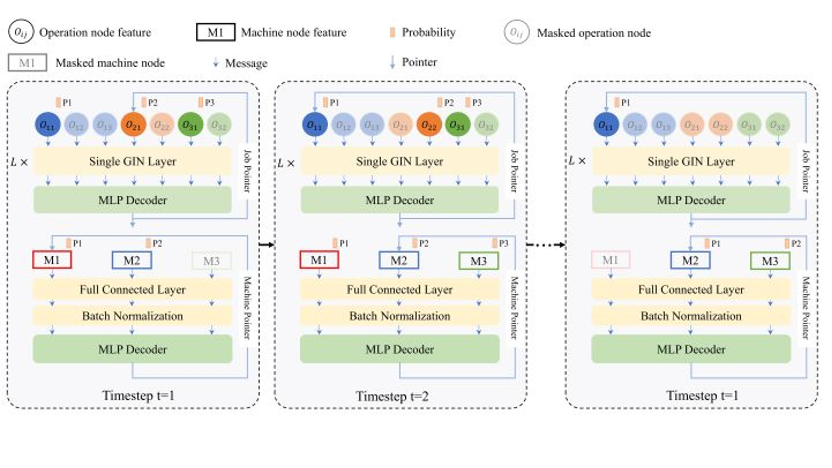
图6 MPGN wolkflow.

该网络适用于 FJSP、列车调度问题等多动作组合优化问题(结构如图7所示)。此外，为训练该网络结构设计基于actor-critic风格的多近端策略优化算法(multi-proximal policy optimization algorithm, multi-PPO)来训练所提出的MPGN。

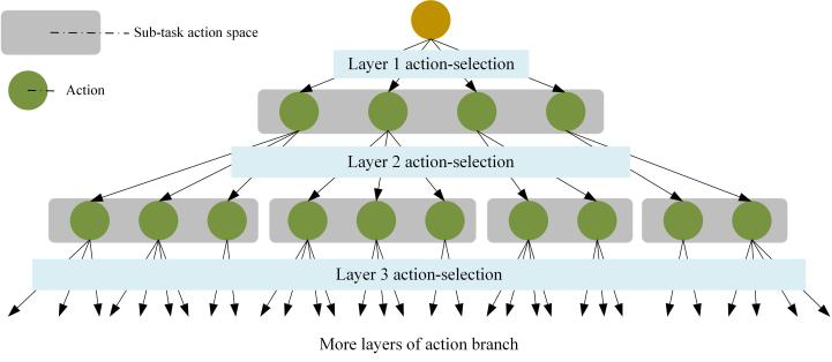
图7 多动作(任务)组合优化问题动作树状结构

具体实现细节及实验结论请参考原文链接。

#-------此外，我们近期还投稿了使用分层强化学习（Hierarchical Reinforcement Learning）端到端地求解动态调度问题的文章，后续也会开源代码，大家感兴趣可以持续关注下

未来智能实验室的主要工作包括：建立AI智能系统智商评测体系，开展世界人工智能智商评测；开展互联网（城市）大脑研究计划，构建互联网（城市）大脑技术和企业图谱，为提升企业，行业与城市的智能水平服务。每日推荐范围未来科技发展趋势的学习型文章。目前线上平台已收藏上千篇精华前沿科技文章和报告。

如果您对实验室的研究感兴趣，欢迎加入未来智能实验室线上平台。扫描以下二维码或点击本文左下角“阅读原文”