今天我们来聊聊物理信息机器学习PIML。PINN大家都熟悉吧,毕竟研究热度就没下去过,这个热点其实就是PIML的一种典型代表。
PIML是一种融合了物理学与机器学习的创新技术,通过引入物理学的先验知识,来改进和优化机器学习模型的性能。这种技术的优点很多,尤其是在数据稀缺或昂贵的领域,不仅能提高数据效率,生成的预测也更符合物理原理,可解释性更高。
因此在金融、医疗、工程等行业,PIML被广泛应用与研究,在学术界也同样是发文高频主题词。这里值得一提的是,最近PIML的一篇成果更是登上了Science正刊!
为了给同学们提供新的发文思路和方向,这次我整理了11个PIML创新方案,原文以及开源代码已附,想冲顶会顶刊的同学抓紧啦。
扫码添加小享,回复“物理机器”
免费获取全部论文+开源代码

【Science正刊】Physics-informed machine learning
方法:论文探讨了物理信息机器学习模型中的新算法和计算框架,旨在解决训练大规模神经网络的非凸优化问题,强调了在多物理和多尺度问题中存在的研究空白,通过引入元学习技术、改进神经网络架构和训练算法来增强模型的稳健性和稳定性,最终为科学计算中的物理建模提供了一种优化的、集成数据与物理知识的创新方法。
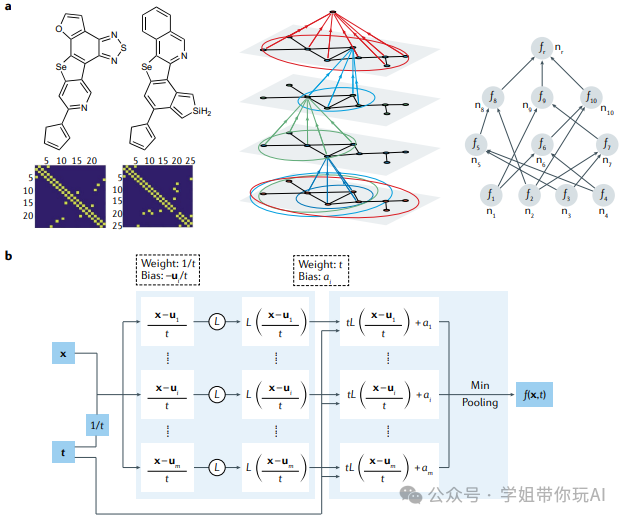
创新点:
- 通过物理启发的学习,可以将物理原理嵌入到机器学习中,以提高模型的训练速度和泛化能力。
- 通过观测数据,可以将物理原理作为训练模型的先验知识,以提供额外的约束和指导。
- 物理方程和物理定律可以用于设计专门的神经网络架构,以更好地满足物理系统的特点和要求。
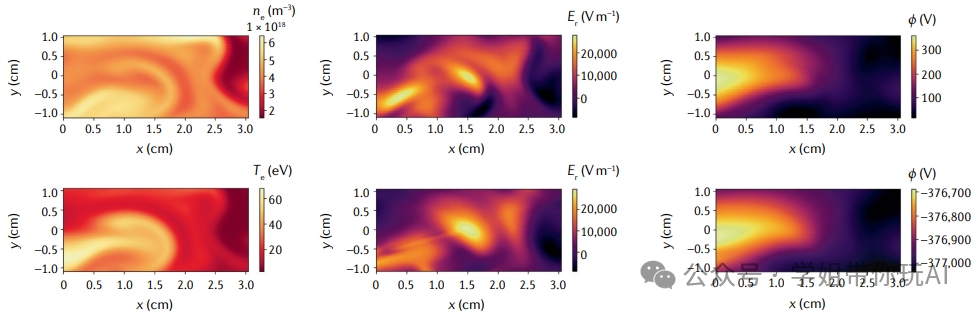
Improving River Routing Using a Differentiable Muskingum-Cunge Model and Physics-Informed Machine Learning
方法:论文介绍了一种新的方法,通过结合可微分的Muskingum-Cunge(MC)模型和物理信息机器学习技术,来改进河流路径模拟的准确性。这种方法通过嵌入一个神经网络来推断Manning粗糙度(n)和河道几何形状,从而提高了河流路径模拟的泛化能力。
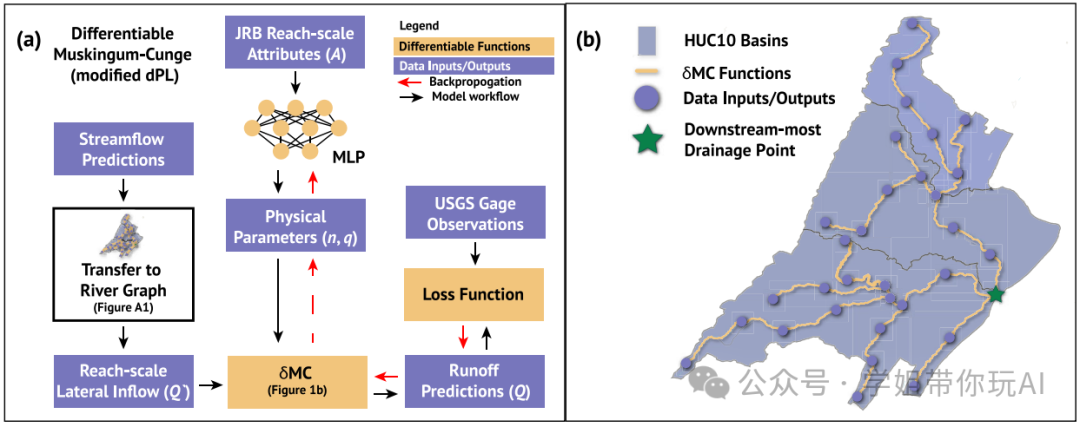
创新点:
- 引入了一种新颖的可微路由方法,结合了经典的Muskingum-Cunge路由模型和神经网络(NN),能够从原始的河段尺度属性中推断曼宁粗糙系数(n)和河道几何形状。
- 开发了一个物理驱动的图神经网络(GNN),通过可微建模框架在河流网络中进行路由,并学习路由流的参数化方案。
扫码添加小享,回复“物理机器”
免费获取全部论文+开源代码

Separable DeepONet: Breaking the Curse of Dimensionality in Physics-Informed Machine Learning
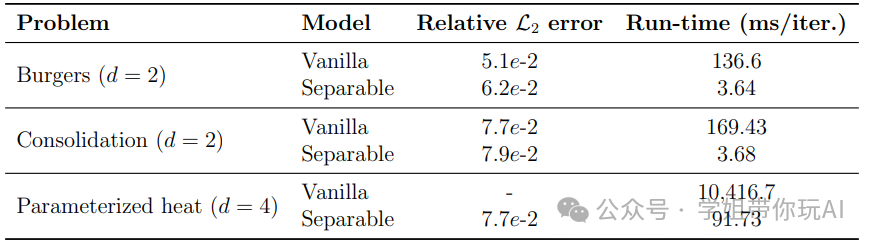
方法:论文研究了分离式DeepONet框架在求解复杂和高维偏微分方程(PDE)中的应用,旨在解决传统框架计算效率低下的问题,通过引入可分离网络结构,显著降低计算成本和提高效率。
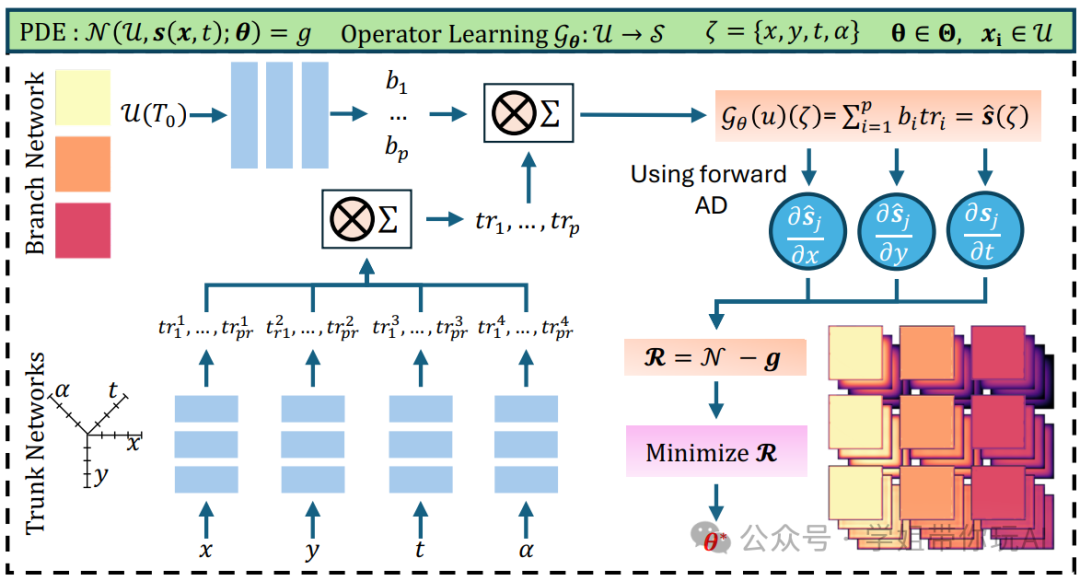
创新点:
- 引入分离技术,通过独立的子网络处理一维坐标,减少前向传递次数和雅可比矩阵大小。
- 采用正向自动微分(AD),优化雅可比矩阵相关的计算成本,实现计算成本随离散化密度线性增长。
- 在物理约束的条件下,将分离技术应用于DeepONet,通过在损失函数中嵌入物理信息来学习系统。
Neural oscillators for generalization of physics-informed machine learning
方法:论文研究了物理信息机器学习(PIML)的泛化能力,特别是在处理以偏微分方程(PDEs)表示的复杂物理问题时。研究通过结合基于常微分方程的神经振荡器与PIML模型,提高了模型在未探索领域的预测准确性。
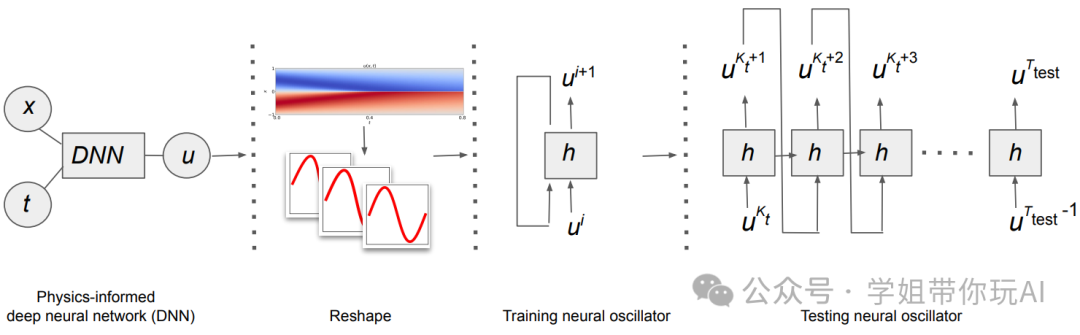
创新点:
- 通过将神经振荡器与物理信息神经网络(PINN)相结合,提升了模型在未探索区域的泛化能力。
- 该方法有效地捕捉了偏微分方程(PDE)解的长期动态特性,超越了现有技术在多种度量上的表现。
- 通过使用基于常微分方程(ODE)的神经振荡器,成功缓解了梯度爆炸和消失问题。
- 这种方法利用PDE解的因果性和时间序列特征,促进了物理信息机器学习任务中的泛化。

扫码添加小享,回复“
物理机器”
免费获取全部论文+开源代码
