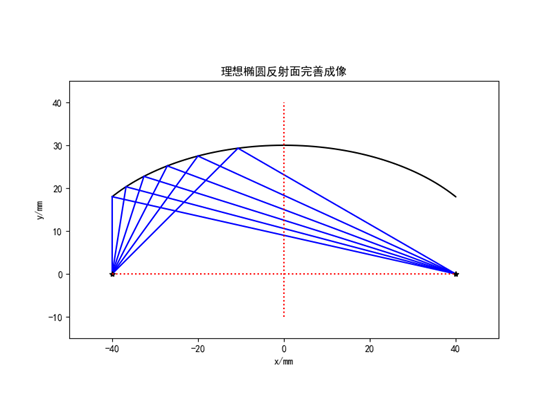
当一个光学系统所获得的像能够与物完全相似,而且每个物点都刚好汇聚于一个像点,这样的成像称为完善成像。
绝大部分光学成像系统设计的目的就是为了获得完善成像。
根据费马原理,如果物点和像点之间的所有光线都能获得相等光程,那么这样的系统既符合光的传播规律,又达到了完善成像条件。
在椭球面反射镜中,对它的两个焦点符合等光程条件,如下图所示:
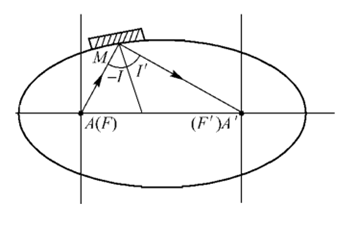
对两定点距离之和等于常数的点的轨迹,是以该两定点为焦点的椭圆。所以,椭球面反射镜对它的两个焦点等光程。
当光程为正时,物点和像点都是实的,对应的反射面为凹面;如果光程为负,物点和像点都是虚的,对应的反射面为凸面。
现在,已知一个镜面为椭球面,光线由A点发出,B点为接收点,如下图所示:
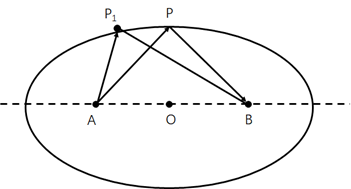
其中各点坐标为A(-40,0),B(40,0),P(0,30),反射镜直径为60mm,在Python中仿真满足条件的反射镜。
(1)用几何的方法仿真
椭圆示意图如下:
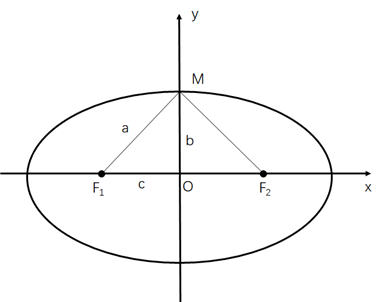
根据解析几何,焦点为F1(-c,0)和F2(c,0)且椭圆满足以下方程:
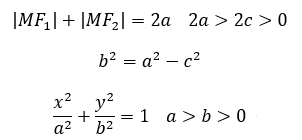
所以当y>0时,
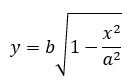
用Python脚本实现如下:
import numpy as np
import matplotlib.pyplot as plt
import math
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 椭圆参数
c = 40
b = 30
a = math.sqrt(b**2 + c**2)
# 椭圆方程
x = np.arange(-40, 40, 0.1)
y = b * np.sqrt(1 - x**2 / a**2)
# 绘制椭圆
plt.plot(x, y, 'k', linewidth=4)
# 画椭球面
x1 = np.arange(-40, 0, 5)
y1 = b * np.sqrt(1 - x1**2 / a**2)
# 绘制椭球面上的点
for i in np.arange(0, len(x1)):
plt.plot([-40, x1[i]], [0, y1[i]],
'b')
plt.plot([40, x1[i]], [0, y1[i]],
'b')
# 绘制坐标轴
plt.plot([-40, 40], [0, 0], '*k')
plt.plot([-40, 40], [0, 0], ':r')
# 绘制y轴
plt.plot([0, 0], [-10, 40], ':r')
# 设置坐标轴比例和标题
ax = plt.gca()
ax.set_aspect('equal')
plt.xlim(-50, 50)
plt.ylim(-15, 45)
plt.title('理想椭圆面镜完善成像')
plt.xlabel('x/mm')
plt.ylabel('y/mm')
# 显示图形
plt.show()
查看结果,如下图:
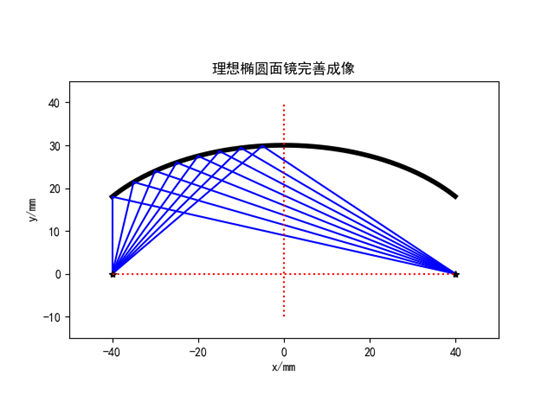
(2)用费马原理仿真
根据费马原理,如果需要完善成像,你们A点发出的任何光线经过反射镜到达B点的光程需要相等。
首先,根据光源A、接收器B和反射镜的位置P计算出光程;然后,设光线角度为θ,并计算Pi,需要满足以下条件:
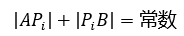
用Python脚本实现如下:
import numpy as np
import matplotlib.pyplot as plt
import math
from scipy.optimize import fsolve
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义计算两点之间距离的函数
def dist(p0, pl):
return math.sqrt(sum((p0 - pl)**2))
#
定义焦点A和B
A = np.array([-40, 0])
B = np.array([40, 0])
# 定义点P
P = np.array([0, 30])
OPL = dist(A, P) + dist(B, P) # 计算总光程
# 初始化点数组
pp = np.array([])
# 角度变化值
for t in np.arange(90, 36.87, -1) / 180 * math.pi:
func = lambda x: np.array([
dist(A, np.array([x[0], x[1]])) +
dist(B, np.array([x[0], x[1]])) - OPL,
(x[0] + 40) * math.sin(t) - x[1]
* math.cos(t)
], dtype=np.float32)
p = fsolve(func, np.array([0, 30],
dtype=np.float32))
pp = np.append(pp, p)
# 重新排列pp数组
pp = np.reshape(pp, [2, -1], order='F')
# 绘制图形
plt.figure(figsize=(8, 6))
# 绘制反射路径
plt.plot(pp[0, :], pp[1, :], 'k')
plt.plot(-pp[0, :], pp[1, :], 'k')
# 计算pp数组的长度
pp_length = pp.shape[1]
# 设置采样因子,以确保不会超出索引范围
sampling_factor = int(pp_length / 6)
# 绘制椭球面上的点
for i in np.arange(0, pp_length, sampling_factor):
plt.plot([-40, pp[0, i]], [0, pp[1,
i]], 'b')
plt.plot([40, pp[0, i]], [0, pp[1,
i]], 'b')
# 绘制坐标轴和焦点
plt.plot([-40, 40], [0, 0], '*k')
plt.plot([-40, 40], [0, 0], ':r')
plt.plot([0, 0], [-10, 40], ':r')
# 设置坐标轴比例和标题
ax = plt.gca()
ax.set_aspect('equal')
plt.xlim(-50, 50)
plt.ylim(-15, 45)
plt.title('理想椭圆反射面完善成像')
plt.xlabel('x/mm')
plt.ylabel('y/mm')
# 显示图形
plt.show()
查看结果,如下图: