大家好,基于Python的数据科学实践课程又到来了,大家尽情学习吧。本期内容主要由春艳与政委联合推出。通过前面的介绍,相信大家对于如何应用statsmodels拟合统计模型得到参数估计以及进行假设检验已经有了一定的了解。接下来就进入statsmodels第三个功能的介绍——进行探索性数据分析。
statsmodels的数据探索功能主要体现在其可视化上,但其可视化功能并不仅仅只能用于进行数据探索,还可以用于模型结果的测试。在第四章中,本书已经介绍了Python中绘图的探索性数据分析的工具。本节的介绍将会是对上一章的一个补充,特别是对于模型结果的可视化诊断。
statsmodels的箱线图主要有两种类型:小提琴图和豆形图。

这里以西安和郑州两座城市团购的购买人数为例,绘制小提琴图进行相应的数据探索和描述。
例1 绘制小提琴图
import statsmodels.graphics.api as smg
city = ['xa', 'zz'] #创建城市列表
buyer = [np.log(model_data['购买人数'][model_data.城市 == c] + 1) for c in city] #生成两座城市购买人数列表
labels = ['xa'
, 'zz'] #设定标签
fig = plt.figure() #创建画布
smg.violinplot(buyer, labels = labels) #绘制小提琴对比图
plt.xlabel("城市") #设置x轴标签
plt.ylabel("log_购买人数") #设置y轴标签
plt.title('西安和郑州购买人数的小提琴图对比') #设置标题
plt.show() #输出图像
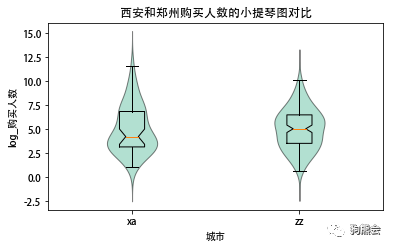
图1 绘制小提琴图
通过小提琴图的对比我们可以得到以下的结论:
通过statsmodels的相关图可以快速直观地探索和描述多个变量之间的相关性。
我们以火锅团购的数值变量为例,进行各数值变量之间相关性的探索和描述。
例2 绘制数值变量的相关图
num_cols = ['评分', '评价数', '人均', '购买人数', '团购价'] #定义数值变量所在列
corr_matrix = np.corrcoef(model_data.loc[:, num_cols].T) #计算数值变量之间的相关系数
smg.plot_corr(corr_matrix, xnames = num_cols) #绘制数值变量之间的相关图
plt.show() #输出图像
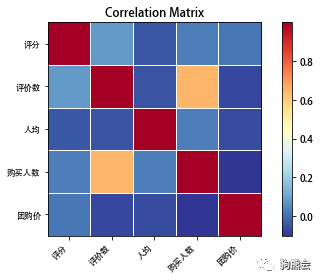
图2 数值变量相关图
从相关图中可以看出:除了评价数与购买人数之间的相关性略强之外,其他各变量之间的相关性都比较弱。
statsmodels可以绘制QQ图来对模型的拟合结果进行诊断。Q-Q图(Q代表分位数)在统计学里是一个概率图,用图形的方式比较两个概率分布,把他们的两个分位数放在一起比较。
QQ图主要用于检验数据分布的相似性。例如利用Q-Q图来对数据进行正态分布的检验,则可以令x轴为正态分布的分位数,y轴为样本分位数。如果这两者构成的点分布在一条直线上,就证明样本数据与正态分布存在线性相关性,即服从正态分布。

这里我们可以针对模型的拟合结果,针对模型的残差来进行正态分布的检验,以此来对模型的拟合情况进行评估。
例3 绘制模型拟合参数的QQ图
import scipy.stats as stats
res = results.resid #获取最小二乘回归拟合模型的残差数据
sm.qqplot(res, stats.t, fit = True, line = '45') #绘制模型残差的qq图,自动确定t分布的参数,包括均值和标准差
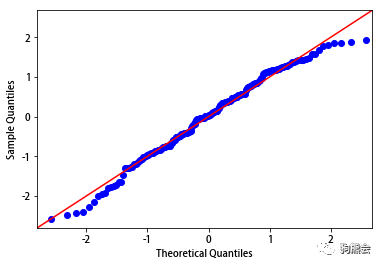
图3 模型残差正态分布检验的QQ图
从图中可以看出:模型残差与正态分布所构成的点几乎除了在两端有些许的异常点之外,几乎都分布在一条直线上,因此认为模型残差通过了正态分布检验,模型满足正态性要求。
利用回归图可以通过偏差图看到在拟合模型下自变量与因变量之间的关系。

这里我们针对前面的最小二乘回归模型,为每个自变量创建一个子图。偏差图中会显示模型中每个变量在去掉其他解释变量的影响后,与对数购买人数的关系。
例4 绘制模型的回归图
fig = plt.figure(figsize=(8, 12)) #设定画布大小
smg.plot_partregress_grid(results_f, fig = fig) #绘制模型中每个自变量与对数购买人数的回归图
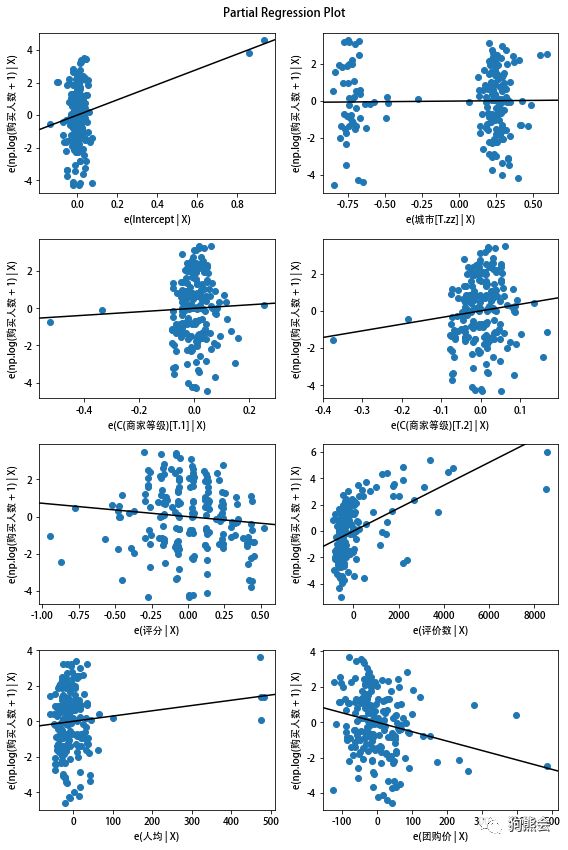
图4 模型回归图
除了以上介绍的四种可视化图形之外,statsmodels还可以提供函数图、时序图、因子水平交互图等多种数据探索以及模型检验的可视化图表,这里就不一一介绍了,如果想要了解更多的话,大家可以去官方文档进行进一步的学习和挖掘。
好了,今天就讲到这里。