变量之间关系可以分为两类：
函数关系：反映了事务之间某种确定性关系
相关关系：两个变量之间存在某种依存关系，但二者并不是一一对应的；反映了事务间不完全确定关系；相关系数(r)可以衡量这种相关关系。
r的取值范围是[-1,1]，r=1表示完全正相关！r=-1表示完全负相关！r=0表示完全不相关。
为什么要对相关系数进行显著性检验？
1）实际上完全没有关系的变量，在利用样本数据进行计算时也可能得到一个较大的相关系数值（尤其是时间序列数值）
2）当样本数较少，相关系数就很大。当样本量从100减少到40后，相关系数大概率会上升，但上升到多少，这个就不能保证了；取决于你的剔除数据原则，还有这组数据真的可能不存在相关性；
改变两列数据的顺序，不会对相关系数，和散点图（拟合的函数曲线）造成影响；
对两列数据进行归一化处理，标准化处理，不会影响相关系数；
我们计算的相关系数是线性相关系数，只能反映两者是否具备线性关系。相关系数高是线性模型拟合程度高的前提；此外相关系数反映两个变量之间的相关性，多个变量之间的相关性可以通过复相关系数来衡量；
线性关系检验
回归系数检验
最小二乘法是一种数学优化技术，它通过最小化误差的平方和寻找数据的最佳函数匹配。
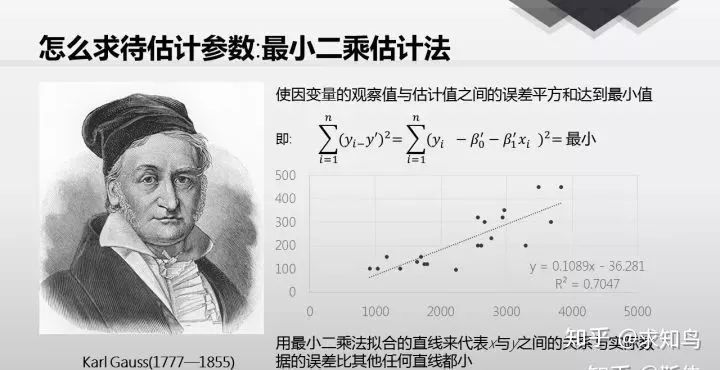
拟合优度：顾名思义，拟合优度就是衡量一个回归做的好不好的指标，定义为 
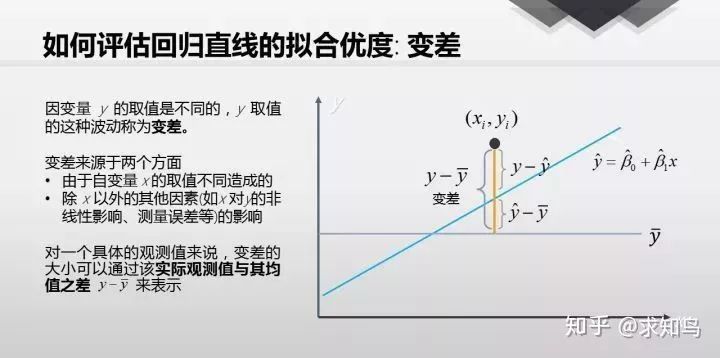
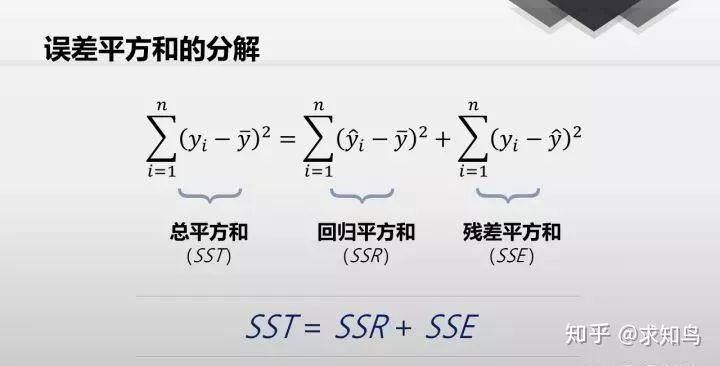
我们期望回归平方和占比越大，那么我们的模型就越好；但是回归平方和<=总平方和；
的缺陷：新增加一个变量，
会加大；所以单独用 来评价模型的好坏并不靠谱
可以联想到P值，我们总是说P<0.05，能得出显著性的结论，我们拒绝H0，接受H1（往往我们对假设进行设计时，H1是我们想要支持的假设，H0是我们反对的假设。）
至于P<0.05的标准，则是统计学家们拍脑袋拍出来的。----人大著名统计学家吴喜之
针对 的缺陷：学者们提出了调整
由此可见，R方总是小于调整R方的且调整R方可能为负；并且只有R方趋近1时，调整R方才有出马的意义！
因此判断多重共线性也多了一个方法：
选择其中一个自变量将其作为因变量，重新拟合，求 ；若 趋近1，则存在多重共线性！
多重共线性：多重共线性与统计假设没有直接关联，但是对于解释多元回归的结果非常重要。相关系数反应两个变量之间的相关性；回归系数是假设其他变量不变，自变量变化一个单位，对因变量的影响，而存在多重共线性（变量之间相关系数很大），就会导致解释困难；比如y~x1+x2；x·1与x2存在多重共线性，当x1变化一个单位，x2不变，对y的影响；而x1与x2高度相关，就会解释没有意义。
一元回归不存在多重共线性的问题；而多元线性回归要摒弃多重共线性的影响；所以要先对所有的变量进行相关系数分析，初步判定是否满足前提---多重共线性
时间序列数据会自发呈现完全共线性问题，所以我们用自回归分析方法；
出现多重共线性如何改善：
1. 删除变量对去除多重共线性最为显著。
2. 不想删除变量，可以对自变量进行降维（CPA主成分分析），主成分分析后的各主成分之间是正交的，所以一定是线性无关。
3. 改善模型。
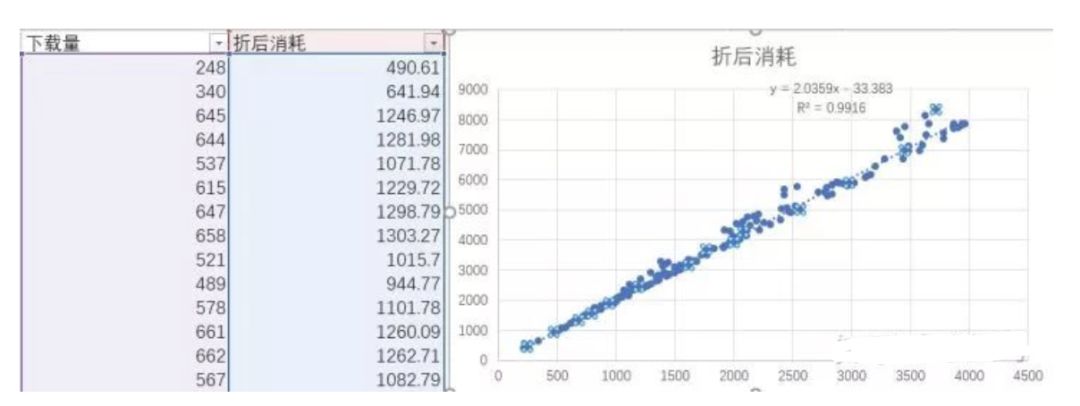
折后消耗y，下载量x
Excel绘制方法：先绘制散点图--右键--添加趋势线
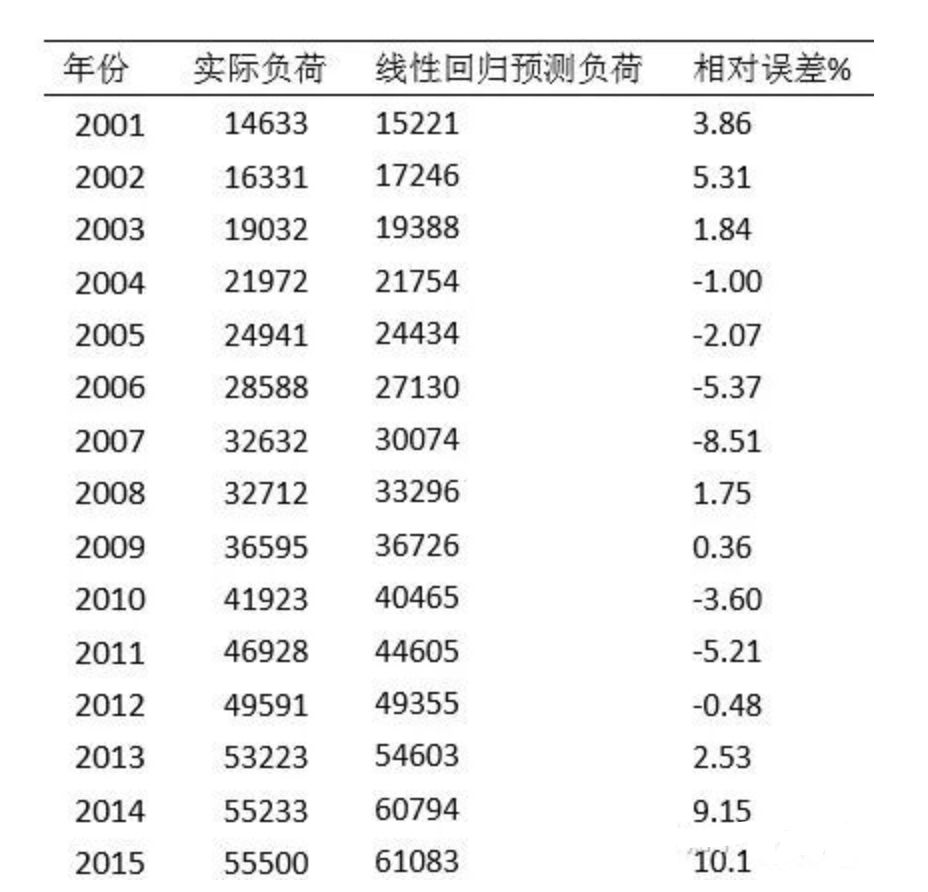
电力系统中长期负荷的变化受到很多因素制约，这种制约关系难以定性描述，征对负荷影 响因素的复杂性和不确定性，即多变量和随机性，笔者将多元回归分析应用到中长期电力负 荷预测之中。因变量（y）为全社会用电量，自变量通常为影响电力负荷各种因素，比如经 济，人口，气候等等，本文选择以国民生产总值 GDP（x1）、全国人口（x2）为自变量，建 立回归方程。考虑到国内五年计划对预测的影响，选择 2001-2015 年的全社会用电量作为样 本。
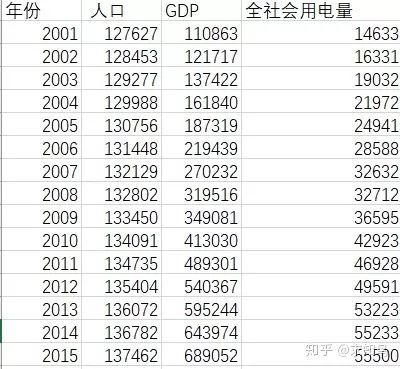
源数据 R语言
datanewdatafitsummary(fit)
回归方程为：
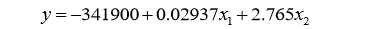
对线性回归方程进行如下假设检验：正态性检验、线性检验、独立性检验、同方差性检 验。
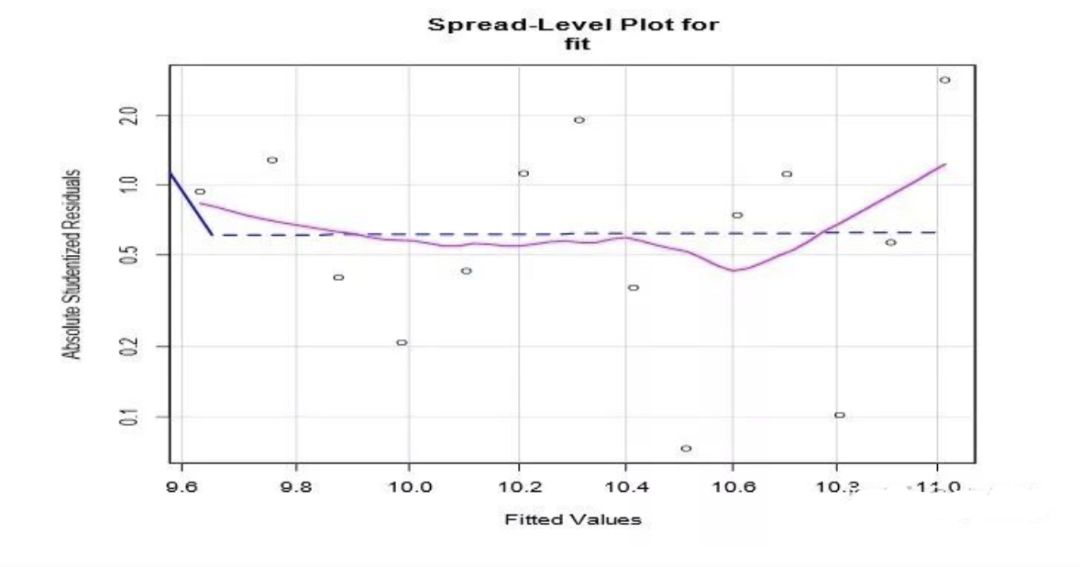
对线性模型进行检验发现该模型不满足同方差假设。同方差检验结果如图 1 所示
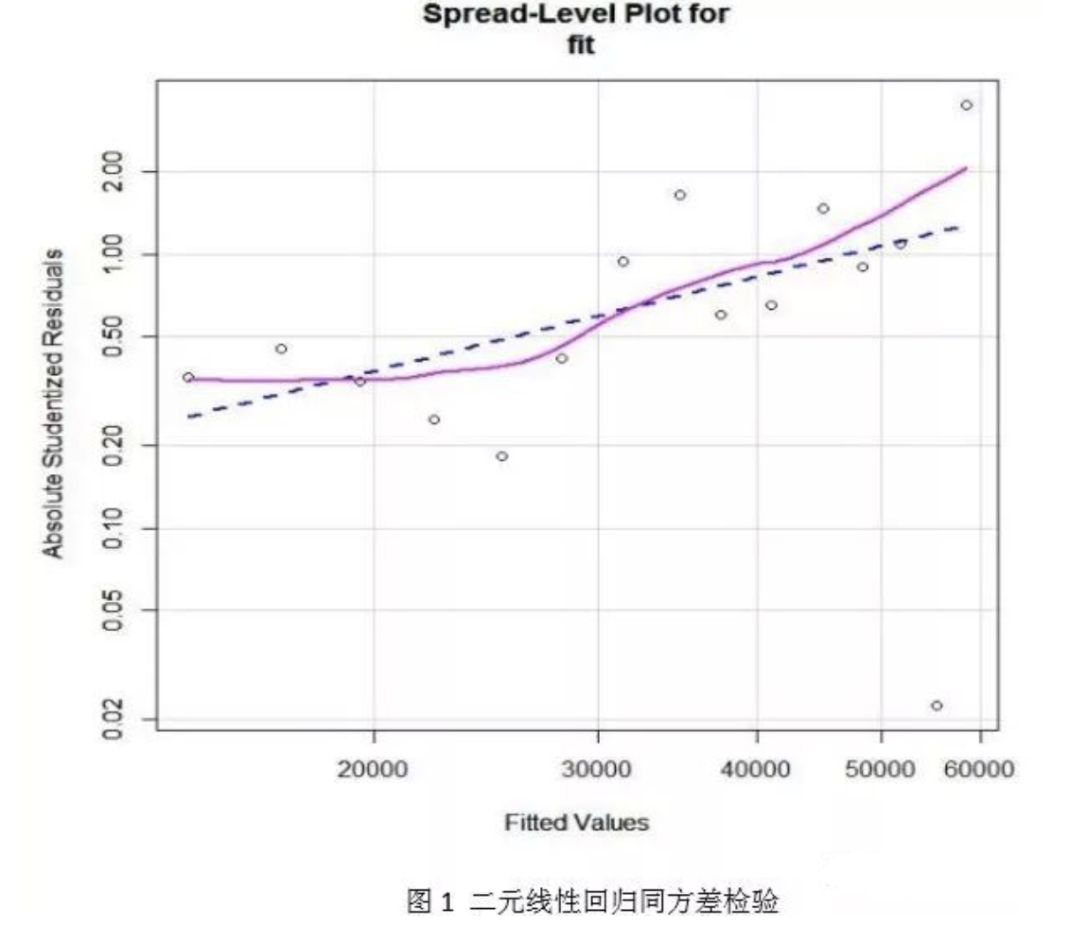
采用 R 软件包提供的 spreadLevelPlot()函数创建了一个添加最佳拟合曲线的散点图，展 示标准化残差绝对值与拟合值的关系。若满足同方差假设，图 1 中点的水平在最佳拟合曲线 周围应该呈水平随机分布，而图 1 显然不是，说明违反了同方差假设。模型不符合同方差假设，通常可以对因变量进行 BOX-COX 变换：
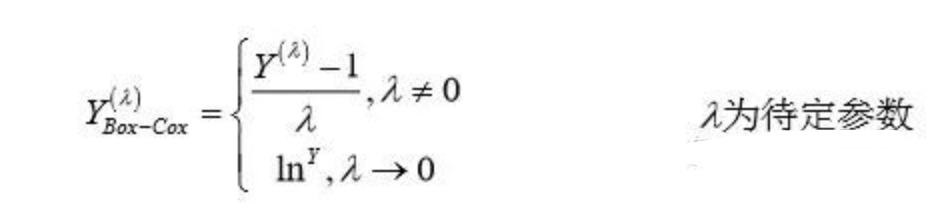
利用 R 软件包提供的 powerTransform()，函数通过最大似然来估计出 
，研究发现对因变 量进行对数变换，去除自变量 GDP （x1）后，拟合效果最好，且满足各种假设检验。
拟合结果如表 3 所示，模型整体解释能力如表 4 所示：
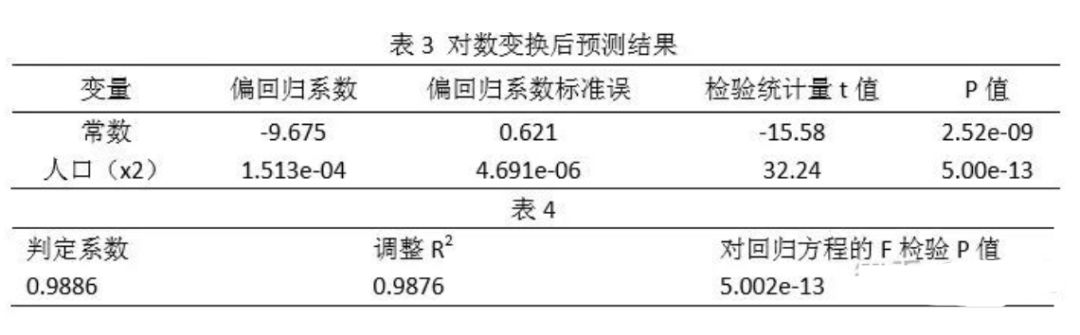
建立的回归方程：
常数项没有物理意义，只是一个常量调整项。人口的回归系数为 0.0001531，表示人口每 增加 1 万人，全社会用电量增加 1.000151 亿千瓦时，它的系数检验 P 值<0.05，表明在 0.05 的显著水平下是显著的。总体来看，人口解释了全社会用电量 98%的方差。对回归方程的 F 检验 p 值<0.05,表明预测变量人口有 95%以上的概率可以预测全社会用电量。
R 软件包中的 qqPlot(),提供了准确的正态假设检验方法，它画出了 n-p-1 个自由度下的 t 分布下的学生化残差图形，其中 n 是样本大小，p 是回归参数的数目（包括截距项）。如图 2 所示：
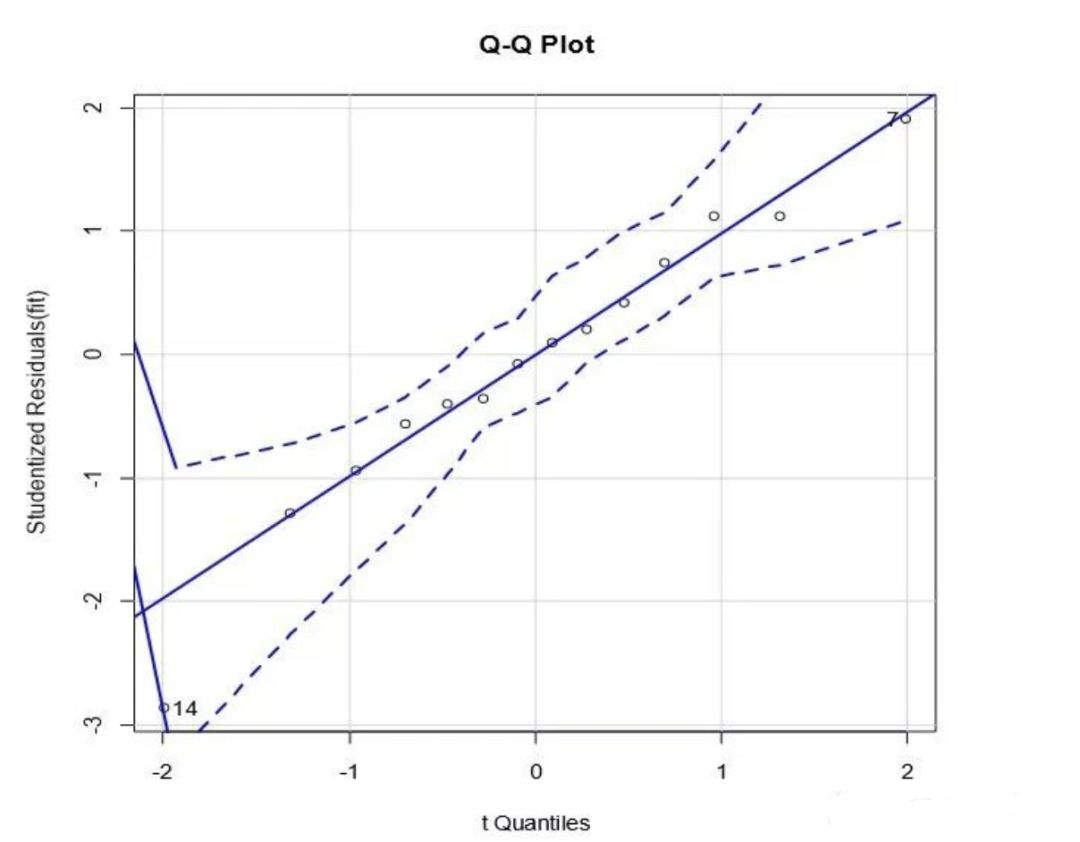
R 软件包中的 Durbin-Watson 检验的函数 durbinWatsonTest()，能够检验出误差的独立 性。经检验 P 值>0.05,不显著。说明误差项之间独立。
R 软件包中的 crPlots()函数绘制的成分残差图，可以检测出因变量与自变量之间是否非线 性关系，检测结果如图 所示：
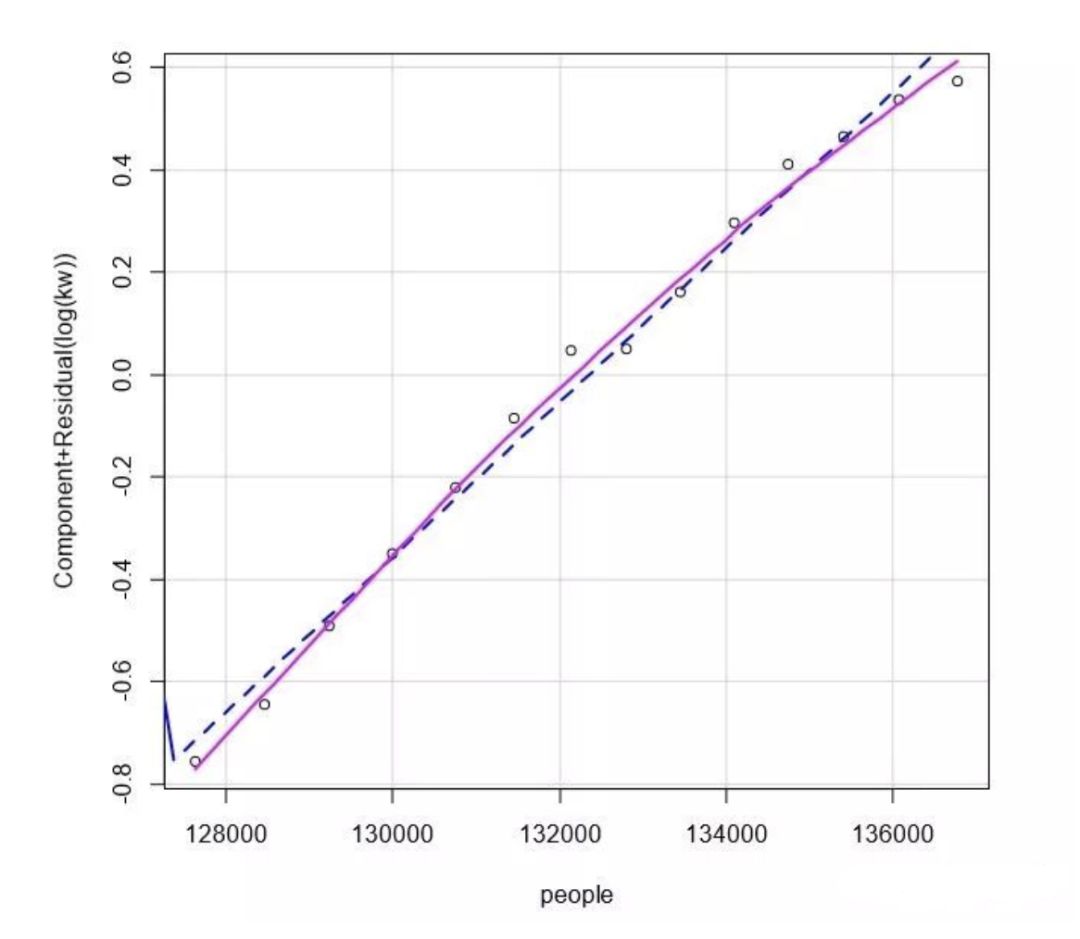
R 软件包中的 spreadLevelPlot()函数创建了一个添加最佳拟合曲线的散点图，展示标准化 残差绝对值与拟合值的关系。若满足同方差假设，图 4 中点的水平在最佳拟合曲线周围应 该呈水平随机分布，结果表明符合同方差假设。
library(car)qqPlot(fit,lables=row.names(newdata),id.method="identify",simulata=TRUE,main=" Q-Q Plot")durbinWatsonTest(fit)crPlots(fit)spreadLevelPlot(fit)ncvTest(fit)##BOX-COX 确定因变量类型函数summary(powerTransform(newdata$kw))##第一种变换fitsummary(fit) ###假设检验 ##第二种变换fitsummary(fit) ###假设检验fitsummary(fit) ##假设检验fitsummary(fit)##假设检验fitsummary(fit)##假设检验y.pre##计算预测值fit2
Python回归
import numpy as npimport pandas as pddata=pd.read_csv("C://Users//baihua//Desktop//vehicles.csv",encoding='utf-8')
df=pd.DataFrame(data)df.columns=["code","date","y","x1","x2","x3","x4","x5","x6","x7"]
'''思考：df=pd.DataFrame(data,columns=["code","date","y","x1","x2","x3","x4","x5","x6","x7"])print(df)
出现NaN的原因：columns是取data中的列而不是重命名，可以调整列中的顺序但不可重命名！'''print(df)df1=df.drop(["code","date"],axis=1) #中文字段名报错，需要修改为英文字段名
探索数据
做一个相关系数矩阵；
多元回归如何选择自变量？相关系数可以判断自变量是否可以预测因变量
补充：选择特征的角度很多：变量的预测能力，变量之间的相关性，变量的简单性（容易生成和使用），变量的强壮性（不容易被绕过），
变量在业务上的可解释性（被挑战时可以解释的通）等等。但是，其中最主要和最直接的衡量标准是变量的预测能力。
1. 特征选择：特征发散，如果一个特征不发散，方差为0，说明样本在这个特征上基本没有差异，这个特征对于样本区分基本没用
2. 特征选择：考虑特征与目标的相关性，优先选择与目标相关性高的特征！
3. 根据方差选择特征：计算各个特征的方差，选择方差大于阈值的特征
4. 单变量特征选择：计算每个特征与y的相关性；对于回归问题或分类问题可以采用卡方检验的方式对特征进行检测
5. 皮尔逊相关系数（适用于回归问题即y连续），简单实用
6. 基于模型的特征融合方法：主成分分析，聚类，支持向量机，随机森林都可以作为筛选特征的方法
'''print(df1.corr())print('---')print(df1.cov())
print(df1.describe())
多元回归的变量选择：
在变量较少的情况下，全子集回归都要优于逐步回归；
但若是变量较多，全子集回归就会很费时间；
变量的自动选择是对模型选择的一种辅助方法，而不是直接方法；
缺陷：只能选出模型拟合度最高的模型，但是该模型是不是有意义，我们还需要结合真实场景进行选择；
from sklearn.model_selection import train_test_splitimport numpy as npfrom sklearn import datasets,linear_modelimport pandas as pd
y=df1.iloc[:,0]x=df1.iloc[:,[1,2,3,4]]
# 训练数据x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.25, random_state = 1)regr = linear_model.LinearRegression()regr.fit(x_train,y_train) #训练拟合参数
print('coefficients(b1,b2...):',regr.coef_)print('intercept(b0):',regr.intercept_)# 预测数据y_pred = regr.predict(x_test)print(y_pred)# 查看模型得分regr.score(x_test, y_test)
Out：coefficients(b1,b2...): [-2.58276362e-04 9.39725239e-04 3.19754647e+00 1.03817588e+00]intercept(b0): -15.518686092501014[513.46916069 820.48073383 595.60053947 112.04429448 548.1450162 618.4632776 271.81001594 368.01305579 660.92674908 575.78325852 523.48195751 545.90176081 718.77749951 501.81849186 360.00269366 808.0881115 578.33083072]
Out[66]:0.9981218281971582
