昨天在课上,我和学生们聊了聊ChatGPT这类生成式AI,并现场展示了一下如今发展到什么水平了。当然我用的是国产模型chatglm(https://chatglm.cn/)。有学生问:这个软件免费吗?

此图由GPT-4生成
肯定免费。或者说,开发者一般会提供一部分资源供用户免费试用。这是因为人工智能的研发离不开大量的数据,而这些数据主要来源于用户的使用过程。这些数据对于改进人工智能算法至关重要。我们常见的人工智能实质上是运用数学和统计方法来进行预测。
利用大量的数据训练机器,使得机器具备了预测能力。其实,这一切背后的核心本质,是“贝叶斯公式”。
贝叶斯
“这门源自赌博机运之科学,必将成为人类知识中最重要的一部分,生活中大多数问题,都将只是概率的问题。”这是被誉为“法国牛顿”的拉普拉斯(1749年-1827年)对于概率论这一当时新兴学科的评价。
那么贝叶斯(1702年-1761年)究竟做了什么?他主要研究的是“逆概率”或“条件概率”问题,这种概率计算方式略有别于我们的直观感受。他在“白球黑球”实验中讨论了这个问题,不仅包括正向计算,也涉及逆向推理。
是这样的,从一个盒子里随机抽球,如果我们知道盒子里球的颜色分布,就能直接计算出抽到某种颜色球的概率。比如,盒子里有10个球,5个白球和5个黑球,抽到白球或黑球的概率都是50%。如果是6白4黑,那么抽到黑球的概率就是40%。
当更复杂的情况如,10个球中有2白8黑,现在随机抽取2个球,得到1黑1白的概率是多少?由于从10个球中抽取2个球共有90种可能性,而其中1黑1白的情况有16种,所以这种情况的概率是16/90,约等于17.5%。通过这些简单的排列组合运算,我们可以计算在10个球的不同颜色分布下,抽取n个球中m个为黑球的概率。这些例子都是正向概率的计算。
不过,当年的贝叶斯更感兴趣的是反过来的“逆概率问题”:如果我们预先并不知道盒子里球的颜色比例,只知道总共有10个球,比如随机抽出3个球,发现是2黑1白,那么如何从这个试验样本推断盒子里白球和黑球的比例呢?
这就是贝叶斯定理的强大之处:
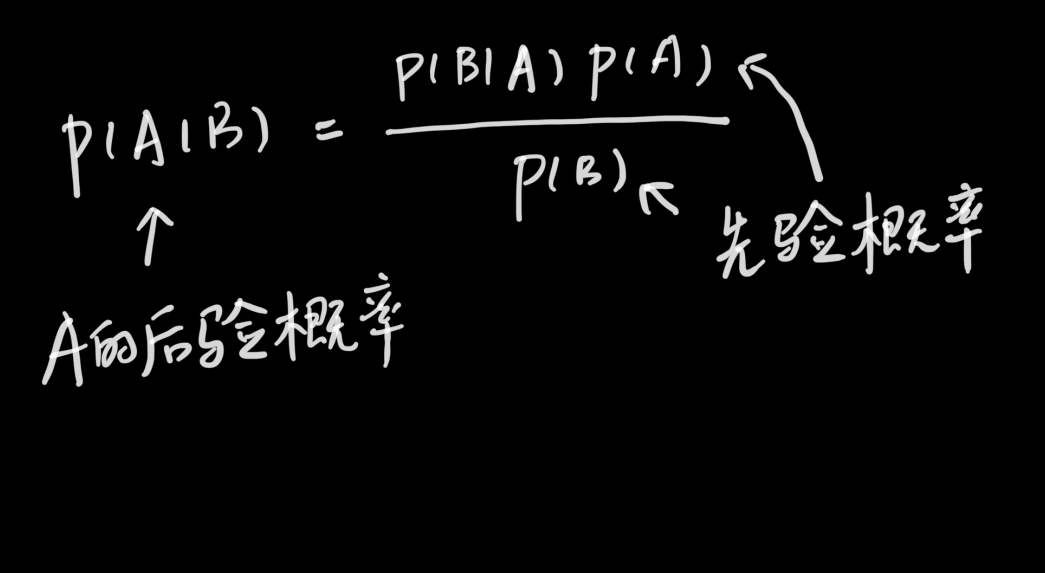
贝叶斯公式
贝叶斯定理的核心在于它允许我们根据观察结果更新对未知概率的估计。简而言之,通过利用事件B发生所带来的新信息,可以修正事件B未发生时对事件A的“先验概率”P(A),从而得到事件B发生时,事件A的“后验概率”P(A|B)。
还是拗口的
举个例子
经典案例:预测天气
小明和小丽是一对热爱冒险的朋友。某个周末,他们约好一起去爬城郊的山,计划在山顶野餐并观赏日落。然而,早上起来,小明发现天空多云,心情顿时变得沉重。
小明说:“小丽,今天我们可能不能去爬山了,天看起来要下雨。”
小丽不甘心,她劝说小明:“别那么悲观,多云不一定会下雨呀!让我给你一些数据。”
大约30%的日子早上是多云的。
城市的天气数据显示,一个月平均只有3天下雨,也就是10%的概率。
60%的雨天早上是多云的。
小明虽然有点担心,但他是个科学爱好者,于是决定用贝叶斯定理来计算当天的降雨概率。
他考虑了以下几点:
根据数据:
贝叶斯定理告诉我们,在早上多云情况下会下雨的概率:P(A|B) = (P(A) * P(B|A)) / P(B)
代入数据:P(A|B) = (0.1 * 0.6) / 0.3 = 0.06 / 0.3 = 0.2
小明计算完毕后,兴致勃勃地看着小丽:“今天下雨的概率是20%。根据这个概率,我们还是有80%的机会不被淋湿。我觉得可以冒一下险,毕竟我们都做好了防雨的准备。”
小丽兴奋地说:“太好了!那我们出发吧!”
最终,他们带上雨具,出发前往远山。尽管天气不完美,但他们在山顶享受到了美好的时光。
换个例子:垃圾邮件过滤
假设我们的目标是判断一封邮件是否为垃圾邮件。我们可以通过分析邮件中是否包含特定的关键词(如“免费”,“奖金”等)来做出判断。在这个例子中:
假设 H 代表一封邮件是垃圾邮件的事件。
E 代表邮件中包含词语“免费”。
根据我们的信息:
垃圾邮件中包含“免费”的概率 P(E|H) 较高,我们假设为 80%。
非垃圾邮件中包含“免费”的概率 P(E|¬H) 较低,我们假设为 20%。
在所有邮件中,垃圾邮件的比例(即先验概率 P(H))假设为 50%。
根据贝叶斯定理,我们可以计算在邮件中出现“免费”这个词的情况下,这封邮件是垃圾邮件的概率 P(H|E):
P(H|E) = (P(E|H) × P(H)) / P(E)
其中 P(E) 是所有邮件中出现“免费”的总概率,这可以通过全概率公式来计算:
P(E) = P(E|H) × P(H) + P(E|¬H) × P(¬H)

全概率公式详见人教版数学选择性必修三7.1
将具体数值代入公式:
P(E) = 0.8 × 0.5 + 0.2 × 0.5 = 0.4 + 0.1 = 0.5
接下来计算 P(H|E):
P(H|E) = (0.8 × 0.5) / 0.5 = 0.8
因此,如果一封邮件中出现了“免费”,那么这封邮件是垃圾邮件的概率为 80%。
ChatGPT的奥秘
到现在为止,不论你明白贝叶斯的公式与否,你都应该懂得了它就是利用大量的“经验”来预测未知的。这就是ChatGPT的底层逻辑。
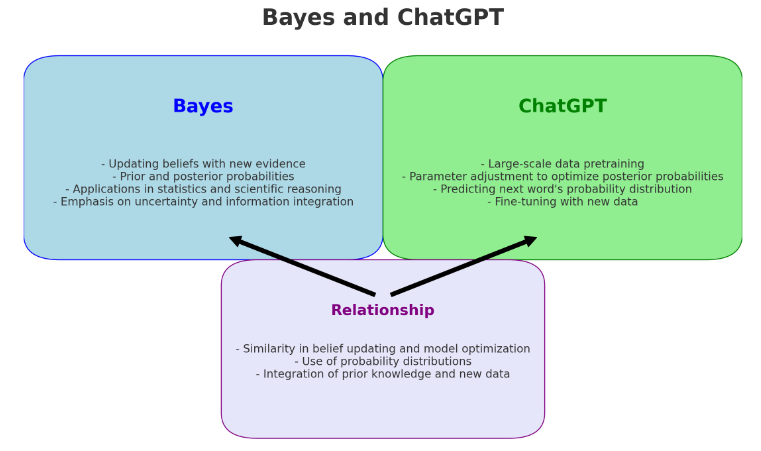
ChatGPT的工作原理可以简单理解为一种高级的“文字接龙”游戏。它通过学习大量的文本数据,掌握了语言的使用规则和模式。当你给它输入一段文字时,它会根据已经学到的知识预测接下来最有可能出现的词或句子。这种预测基于统计概率,利用复杂的数学模型和大量的计算资源来进行。
在训练过程中,ChatGPT类模型通过调整网络参数来优化后验概率,即在给定输入(如一系列单词)的情况下,输出正确下一个单词的概率。这种方法在本质上类似于贝叶斯主义,通过观察数据来更新对世界状态的信念。模型通过大量的数据训练,不断调整和优化,使其能够在不同的上下文中生成合适的响应。
ChatGPT使用的Transformer架构(当下最火的大模型底层架构)在处理输入时,实质上是在评估多个概率分布,每个分布代表在给定上下文中可能生成的下一个单词的概率。通过这种方式,模型使用概率来指导决策和预测,与贝叶斯方法中使用概率整合不确定性和信息的方式大同小异。模型通过计算每个可能单词的概率,选择最合适的单词进行生成,从而生成连贯和合理的文本。
虽然ChatGPT在操作时不显式地定义先验概率,但其预训练过程(在大量数据上学习语言模式)实际上可以看作是在建立一个广泛的先验知识库。这些知识随后在特定任务(如细微的文本生成或问题回答)的微调过程中被进一步精细化。这与贝叶斯更新过程中根据新证据调整先验信念的方法相似。
通过不断吸收和应用新数据,模型不断优化和提升其语言生成能力,使其不断具有像人一样的语言表达。
哲学与贝叶斯主义
贝叶斯主义不仅在统计学和机器学习中发挥重要作用,在哲学中也有深刻的内涵和应用。它涉及到一个终极问题:确定性---我们究竟应该如何理解和处理不确定性、信念更新以及科学?
贝叶斯主义的核心理念是通过观察和新证据来更新对世界的信念。这个过程通过贝叶斯定理实现,用系统化的方法来根据新信息调整原有的先验概率。先验概率代表了在观察新数据之前对某事件发生可能性的初始估计,而后验概率则是结合新证据后得到的更新估计。
在哲学中,贝叶斯主义强调了理性信念更新的机制。哲学家们通过贝叶斯主义讨论如何在面对新信息时理性地调整信念系统。比如,当科学家进行实验并获得新数据时,他们需要根据这些数据来更新对某个理论的支持度。这种更新过程本质上是贝叶斯主义的应用。
进一步说,贝叶斯主义在哲学中探讨了信念的度量问题。传统的逻辑学通常处理的是二值逻辑(某个命题要么真要么假),而贝叶斯主义提供了一种更细腻的方式,使用概率来表示信念的强度。这种处理方式使得我们能够更灵活地描述和分析现实世界中的不确定性。
如此看来,贝叶斯主义无处不在。
参考文献:
知识分子.. ChatGPT的胜利,是概率论的胜利,也是贝叶斯定理的胜利. 公众号:知识分子.
量子学派.. 封杀这个公式,ChatGPT智商将为零. 公众号:量子学派.
黄黎原 (Lê Nguyên Hoang). (2021-3). 贝叶斯的博弈:数学、思维与人工智能. 图灵|人民邮电出版社