“ 深度神经网络模型训练之难众所周知，其中一个重要的现象就是 Internal Covariate Shift. Batch Normalization 大法自 2015 年由Google 提出之后，就成为深度学习必备之神器。自 BN 之后， Layer Norm / Weight Norm / Cosine Norm 等也横空出世。本文从 Normalization 的背景讲起，用一个公式概括 Normalization 的基本思想与通用框架，将各大主流方法一一对号入座进行深入的对比分析，并从参数和数据的伸缩不变性的角度探讨 Normalization 有效的深层原因。”
本文是该系列的第二篇。上一篇请移步：
详解深度学习中的Normalization，不只是BN（1）
主流 Normalization 方法梳理
在上一节中，我们提炼了 Normalization 的通用公式：
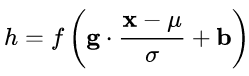
对照于这一公式，我们来梳理主流的四种规范化方法。
3.1 Batch Normalization —— 纵向规范化
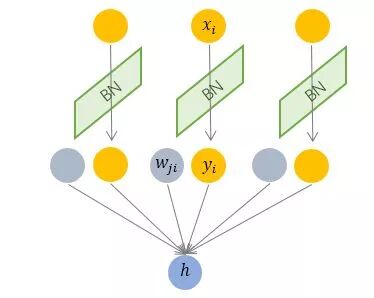
Batch Normalization 于2015年由 Google 提出，开 Normalization 之先河。其规范化针对单个神经元进行，利用网络训练时一个 mini-batch 的数据来计算该神经元 x_i 的均值和方差,因而称为 Batch Normalization。
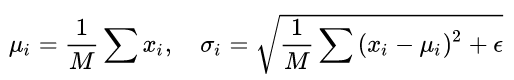
其中 M 是 mini-batch 的大小。
按上图所示，相对于一层神经元的水平排列，BN 可以看做一种纵向的规范化。由于 BN 是针对单个维度定义的，因此标准公式中的计算均为 element-wise 的。
BN 独立地规范化每一个输入维度 x_i ，但规范化的参数是一个 mini-batch 的一阶统计量和二阶统计量。这就要求 每一个 mini-batch 的统计量是整体统计量的近似估计，或者说每一个 mini-batch 彼此之间，以及和整体数据，都应该是近似同分布的。分布差距较小的 mini-batch 可以看做是为规范化操作和模型训练引入了噪声，可以增加模型的鲁棒性；但如果每个 mini-batch的原始分布差别很大，那么不同 mini-batch 的数据将会进行不一样的数据变换，这就增加了模型训练的难度。
因此，BN 比较适用的场景是：每个 mini-batch 比较大，数据分布比较接近。在进行训练之前，要做好充分的 shuffle. 否则效果会差很多。
另外，由于 BN 需要在运行过程中统计每个 mini-batch 的一阶统计量和二阶统计量，因此不适用于 动态的网络结构 和 RNN 网络。不过，也有研究者专门提出了适用于 RNN 的 BN 使用方法，这里先不展开了。
3.2 Layer Normalization —— 横向规范化
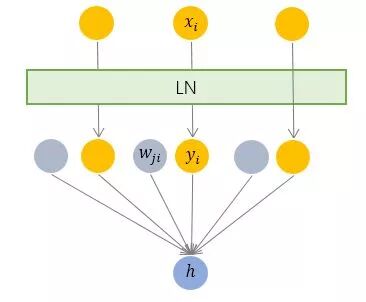
层规范化就是针对 BN 的上述不足而提出的。与 BN 不同，LN 是一种横向的规范化，如图所示。它综合考虑一层所有维度的输入，计算该层的平均输入值和输入方差，然后用同一个规范化操作来转换各个维度的输入。
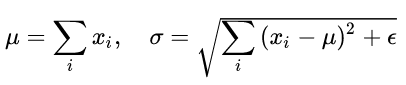
其中 i 枚举了该层所有的输入神经元。对应到标准公式中，四大参数 μ, σ , b, g均为标量（BN中是向量），所有输入共享一个规范化变换。
LN 针对单个训练样本进行，不依赖于其他数据，因此可以避免 BN 中受 mini-batch 数据分布影响的问题，可以用于 小mini-batch场景、动态网络场景和 RNN，特别是自然语言处理领域。此外，LN 不需要保存 mini-batch 的均值和方差，节省了额外的存储空间。
但是，BN 的转换是针对单个神经元可训练的——不同神经元的输入经过再平移和再缩放后分布在不同的区间，而 LN 对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别（比如颜色和大小），那么 LN 的处理可能会降低模型的表达能力。
3.3 Weight Normalization —— 参数规范化
前面我们讲的模型框架
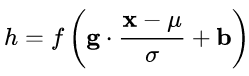
中，经过规范化之后的 y 作为输入送到下一个神经元，应用以 w 为参数的f_w() 函数定义的变换。最普遍的变换是线性变换，即
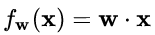
BN 和 LN 均将规范化应用于输入的特征数据 x ，而 WN 则另辟蹊径，将规范化应用于线性变换函数的权重 w ，这就是 WN 名称的来源。
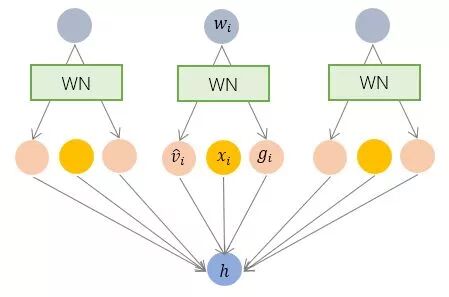
具体而言，WN 提出的方案是，将权重向量 w 分解为向量方向 v 和向量模 g 两部分：
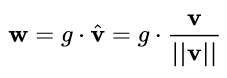
其中 v 是与 g 同维度的向量， ||v||是欧式范数，因此 v / ||v|| 是单位向量，决定了 w
的方向；g 是标量，决定了 w 的长度。由于 ||w|| = |g| ，因此这一权重分解的方式将权重向量的欧氏范数进行了固定，从而实现了正则化的效果。
乍一看，这一方法似乎脱离了我们前文所讲的通用框架？
并没有。其实从最终实现的效果来看，异曲同工。我们来推导一下看。
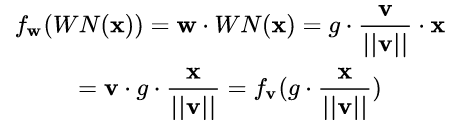
对照一下前述框架：
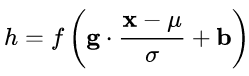
我们只需令：
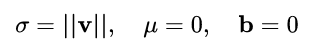
就完美地对号入座了！
回忆一下，BN 和 LN 是用输入的特征数据的方差对输入数据进行 scale，而 WN 则是用 神经元的权重的欧氏范式对输入数据进行 scale。虽然在原始方法中分别进行的是特征数据规范化和参数的规范化，但本质上都实现了对数据的规范化，只是用于 scale 的参数来源不同。
另外，我们看到这里的规范化只是对数据进行了 scale，而没有进行 shift，因为我们简单地令 μ = 0. 但事实上，这里留下了与 BN 或者 LN 相结合的余地——那就是利用 BN 或者 LN 的方法来计算输入数据的均值 μ。
WN 的规范化不直接使用输入数据的统计量，因此避免了 BN 过于依赖 mini-batch 的不足，以及 LN 每层唯一转换器的限制，同时也可以用于动态网络结构。
3.4 Cosine Normalization —— 余弦规范化
Normalization 还能怎么做？
我们再来看看神经元的经典变换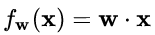
对输入数据 x 的变换已经做过了，横着来是 LN，纵着来是 BN。
对模型参数 w 的变换也已经做过了，就是 WN。
好像没啥可做的了。
然而天才的研究员们盯上了中间的那个点，对，就是 ·
他们说，我们要对数据进行规范化的原因，是数据经过神经网络的计算之后可能会变得很大，导致数据分布的方差爆炸，而这一问题的根源就是我们的计算方式——点积，权重向量 w 和 特征数据向量 x 的点积。向量点积是无界（unbounded）的啊！
那怎么办呢？我们知道向量点积是衡量两个向量相似度的方法之一。哪还有没有其他的相似度衡量方法呢？有啊，很多啊！夹角余弦就是其中之一啊！而且关键的是，夹角余弦是有确定界的啊，[-1, 1] 的取值范围，多么的美好！仿佛看到了新的世界！
于是，Cosine Normalization 就出世了。他们不处理权重向量 w ，也不处理特征数据向量 x ，就改了一下线性变换的函数：
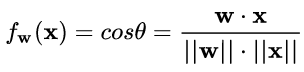
其中 θ 是 w 和 x 的夹角。然后就没有然后了，所有的数据就都是 [-1, 1] 区间范围之内的了！
不过，回过头来看，CN 与 WN 还是很相似的。我们看到上式中，分子还是 w 和 x 的内积，而分母则可以看做用 w 和 x 二者的模之积进行规范化。对比一下 WN 的公式：
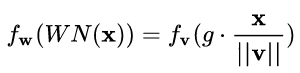
一定程度上可以理解为，WN 用 权重的模 ||v|| 对输入向量进行 scale，而 CN 在此基础上用输入向量的模 ||x|| 对输入向量进行了进一步的 scale.
CN 通过用余弦计算代替内积计算实现了规范化，但成也萧何败萧何。原始的内积计算，其几何意义是 输入向量在权重向量上的投影，既包含 二者的夹角信息，也包含 两个向量的scale信息。去掉scale信息，可能导致表达能力的下降，因此也引起了一些争议和讨论。具体效果如何，可能需要在特定的场景下深入实验。
现在，BN, LN, WN 和 CN 之间的来龙去脉是不是清楚多了？
Normalization 为什么会有效
我们以下面这个简化的神经网络为例来分析。
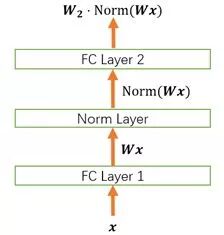
4.1 Normalization 的权重伸缩不变性
权重伸缩不变性（weight scale invariance）指的是，当权重 W 按照常量 λ 进行伸缩时，得到的规范化后的值保持不变，即：
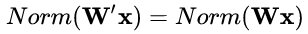
其中 W' = λW 。
上述规范化方法均有这一性质，这是因为，当权重 W 伸缩时，对应的均值和标准差均等比例伸缩，分子分母相抵。
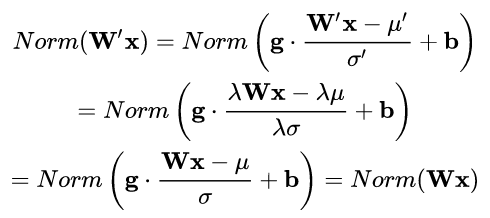
权重伸缩不变性可以有效地提高反向传播的效率。由于
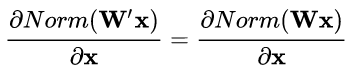
因此，权重的伸缩变化不会影响反向梯度的 Jacobian 矩阵，因此也就对反向传播没有影响，避免了反向传播时因为权重过大或过小导致的梯度消失或梯度爆炸问题，从而加速了神经网络的训练。
权重伸缩不变性还具有参数正则化的效果，可以使用更高的学习率。由于：
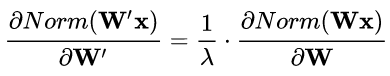
因此，下层的权重值越大，其梯度就越小。这样，参数的变化就越稳定，相当于实现了参数正则化的效果，避免参数的大幅震荡，提高网络的泛化性能。进而可以使用更高的学习率，提高学习速度。
4.2 Normalization 的数据伸缩不变性
数据伸缩不变性（data scale invariance）指的是，当数据 x 按照常量 λ 进行伸缩时，得到的规范化后的值保持不变，即：
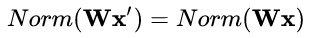
其中 x' = λx 。
数据伸缩不变性仅对 BN、LN 和 CN 成立。因为这三者对输入数据进行规范化，因此当数据进行常量伸缩时，其均值和方差都会相应变化，分子分母互相抵消。而 WN 不具有这一性质。
数据伸缩不变性可以有效地减少梯度弥散，简化对学习率的选择。
对于某一层神经元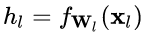
而言，展开可得
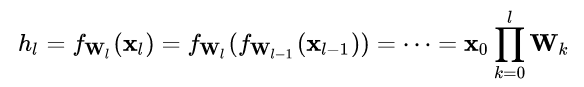
每一层神经元的输出依赖于底下各层的计算结果。如果没有正则化，当下层输入发生伸缩变化时，经过层层传递，可能会导致数据发生剧烈的膨胀或者弥散，从而也导致了反向计算时的梯度爆炸或梯度弥散。
加入 Normalization 之后，不论底层的数据如何变化，对于某一层神经元 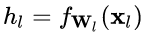而言，其输入 x_l 永远保持标准的分布，这就使得高层的训练更加简单。从梯度的计算公式来看：
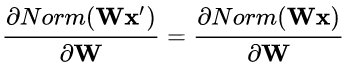
数据的伸缩变化也不会影响到对该层的权重参数更新，使得训练过程更加鲁棒，简化了对学习率的选择。
@Julius
PhD 毕业于 THU 计算机系。
现在 Tencent AI 从事机器学习和个性化推荐研究与 AI 平台开发工作。
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。
▽ 点击 | 阅读原文 | 加入社区
